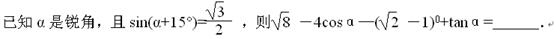题目内容
在Rt
中，∠F="90°，点B、C分别在AD、FD上，以AB为直径的半圆O" 过点C，
联结AC，将△AFC 沿AC翻折得
，
且点E恰好落在直径AB上.
（1）判断：直线FC与半圆O的位置关系是________
_____
__；并证明你的结论.
（2）若OB="BD=2,求CE的长．"
中，∠F="90°，点B、C分别在AD、FD上，以AB为直径的半圆O" 过点C，联结AC，将△AFC 沿AC翻折得
，且点E恰好落在直径AB上.（1）判断：直线FC与半圆O的位置关系是________
_______；并证明你的结论.（2）若OB="BD=2,求CE的长．"
（
1）直线FC与⊙O的位置关系是_相切_；…
……………1’
证明：联结OC
∵OA=OC，∴∠1=∠2，由翻折得，∠1=∠3，∠F=∠AEC=90°
∴∠3="∠2 " ……………………………………………………2’
∴OC∥AF，∴∠F="∠OCD=90°，∴FC与⊙O相切 " …………3’
（2）在Rt△OCD中，cos∠COD=
∴∠COD="60° " …………………………4’
在R
t△OCD中，C
E=OC
·sin∠COD=
………………………5’
1）直线FC与⊙O的位置关系是_相切_；………………1’证明：联结OC
∵OA=OC，∴∠1=∠2，由翻折得，∠1=∠3，∠F=∠AEC=90°
∴∠3="∠2 " ……………………………………………………2’
∴OC∥AF，∴∠F="∠OCD=90°，∴FC与⊙O相切 " …………3’
（2）在Rt△OCD中，cos∠COD=
∴∠COD="60° " …………………………4’
在R
t△OCD中，CE=OC·sin∠COD= ………………………5’略
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
长的直线型通道，中国馆位于世博轴的一侧（如下图所示）. 现测得中国馆到世博轴两端的距离相等，并且从中国馆看世博轴两端的视角为
. 据此数据计算，求：中国馆到世博轴其中一端的距离是多少？.
≈1.73）．
，AB=18，D是边AB上的中点，G是△ABC的重心，那
