��Ŀ����
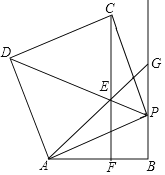
����Ŀ����ͼ��ֱ��l��y=��3x+3��x�ᡢy��ֱ��ཻ��A��B���㣬������y=ax2��2ax+a+4��a��0��������B��
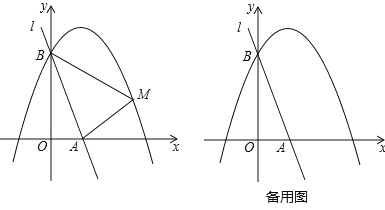
��1����������ߵĺ�������ʽ��
��2����֪��M���������ϵ�һ�����㣬���ҵ�M�ڵ�һ�����ڣ�����AM��BM�����M�ĺ�����Ϊm����ABM�����ΪS����S��m�ĺ�������ʽ�������S�����ֵ��
��3���ڣ�2���������£���Sȡ�����ֵʱ������M��Ӧ��λ�ü�Ϊ��M����
��д����M�������ꣻ
�ڽ�ֱ��l�Ƶ�A��˳ʱ�뷽����ת�õ�ֱ��l������ֱ��l����ֱ��AM���غ�ʱֹͣ��ת������ת�����У�ֱ��l�����߶�BM�����ڵ�C�����B��M����ֱ��l���ľ���ֱ�Ϊd1��d2����d1+d2���ʱ����ֱ��l����ת�ĽǶȣ�����BAC�Ķ�������
���𰸡���1��y=��x2+2x+3����2��S=-![]() m2+
m2+![]() m�����ֵΪ
m�����ֵΪ![]() ����3���٣�
����3���٣�![]() ��
��![]() ������45��.
������45��.
��������
��1����x=0����y=��3x+3��
��y=3��
��B��0��3������B��0��3������y=ax2��2ax+a+4��
��3=a+4��
��a=��1��
����κ�������ʽΪ��y=��x2+2x+3��
��2����y=0ʱ��0=��x2+2x+3��
��x=��1��3��
����������x��Ľ��������Ϊ��1��3��
��0��m��3��
��y=0����y=3x+3��
��x=1��
��A������Ϊ(1,0)��
������֪��M������Ϊ��m����m2+2m+3����
S=S�ı���OAMBS��AOB=S��OBM+S��OAMS��AOB=![]() ��m��3+
��m��3+![]() ��1��(��m2+2m+3)
��1��(��m2+2m+3)![]() ��1��3=
��1��3=![]() (m
(m![]() )2+
)2+![]()
�൱m=![]() ʱ,Sȡ�����ֵ
ʱ,Sȡ�����ֵ![]() .
.
��3�����ɣ�2����֪��M��������Ϊ��![]() ��
��![]() ����
����
�ڹ���M����ֱ��l1��l��������B��BF��l1�ڵ�F��������֪��d1+d2=BF��
�ߡ�BFM��=90����
���F����BM��Ϊֱ����Բ�ϣ���ֱ��AM�����Բ�ཻ�ڵ�H��
�ߵ�C���߶�BM���ϣ�
��F���Ż�BM��H�ϣ�
�൱F��M���غ�ʱ��BF��ȡ�����ֵ����ʱBM����l1��
��A��1��0����B��0��3����M����![]() ��
��![]() ����
����
���ɹ��ɶ�������ã�AB=![]() ��M��B=
��M��B=![]() ��M��A=
��M��A=![]() ��
��
����M����M��G��AB�ڵ�G����BG=x��
���ɹ��ɶ����ɵã�M��B2��BG2=M��A2��AG2��
��![]() ����
����![]() ��x��2=
��x��2=![]() ��x2��
��x2��
��x=![]() ��
��
cos��M��BG=![]() ��
��
��l1��l����
���BCA=90������BAC=45��.


 ������ϵ�д�
������ϵ�д�