题目内容
【题目】自学：如图1，△ABC中，D是BC边上一点，则△ABD与△ADC有一个相同的高，它们的面积之比等于相应的底之比，记为 
= 
．
（△ABD，△ADC的面积分别用记号S△ABD ， S△ADC表示）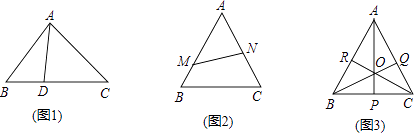
（1）心得：如图1，若BD= 
DC，则S△ABD：S△ADC=
（2）成长：如图2，△ABC中，M，N分别是AB，AC边上一点，且有AM：MB=2：1，AN：NC=1：1，则△AMN与△ABC的面积比为 ．
（3）巅峰：如图3，△ABC中，P，Q，R分别是BC，CA，AB边上的点，且AP，BQ，CR相交于点O，现已知△BPO，△PCO，△COQ，△AOR的面积依次为40，30，35，84，求△ABC的面积．
【答案】
（1）1:2
（2）1:3
（3）
解：设△BRO和△AOQ的面积分别为x、y，
∵△BPO，△PCO的面积分别为40，30，
∴ 
= 
，
∴ 
= ，即 
= ，
=2，
∴OB=2OQ，
∴ 
=2，即 
=2，
则 
，
解得， 
，
∴△ABC的面积为：40+30+35+84+60+72=321
【解析】解：心得：∵BD= 
DC，
∴ 
= ，
∴S△ABD：S△ADC=1：2，
所以答案是：1：2；
成长：如图②．连接BN，
∵AN：NC=1：1，
∴S△ANB=S△CNB= S△ABC ，
∵AM：MB=2：1，
∴SAMN= 
S△ANB ，
∴△AMN与△ABC的面积比为1：3，
所以答案是：1：3；
巅峰：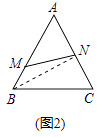
【考点精析】本题主要考查了相似三角形的应用的相关知识点，需要掌握测高：测量不能到达顶部的物体的高度，通常用“在同一时刻物高与影长成比例”的原理解决；测距：测量不能到达两点间的举例，常构造相似三角形求解才能正确解答此题．
练习册系列答案
相关题目
