题目内容
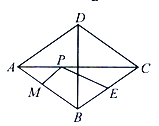
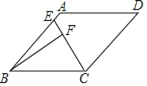
【题目】如图,在菱形ABCD中,∠ABC=45°,AB=4,点E是AB边上的动点,过点B作直线CE的垂线,垂足为点F.
(1)当点F落在AB上时,求∠BCF的度数;
(2)若∠EBF=15°,求CF的长;
(3)当点E从点A运动到点B时,求点F运动的路径长.
【答案】(1)∠BCF=45°(2)2或2![]() (3)
(3)![]()
【解析】分析:(1)根据等腰直角三角形的性质即可解决问题;
(2)分以下两种情况:①当点F在菱形内部时,②当点F在菱形外部时;
(3)首先确定点F的运动轨迹,利用弧长公式计算即可;
详解:(1)当点F落在AB上时,点E,F重合,即CF⊥AB.
∵∠ABC=45°,∴∠BCF=45°.
(2)分以下两种情况:
①当点F在菱形内部时,∠FBC=45°﹣15°=30°.在Rt△BFC中,BC=4,∠FBC=30°,sin30°=![]() =
=![]() ,∴CF=2;
,∴CF=2;
②当点F在菱形外部时,∠FBC=15°+45°=60°.在Rt△BFC中,BC=4,sin60°=![]() =
=![]() ,∴CF=2
,∴CF=2![]() .
.
故CF的长为2或2![]() .
.
(3)如图,设BC的中点为点O,以点O为圆心,OB长为半径画半圆O,连
接 AC,BD交于点F′,易得点F′在半圆O上,连接OF′.
∵BF⊥CE,∴∠BFC=90°,∴点F在半圆O中的一段弧上运动,当点E从点A运动到点B时,点F的运动路径的长为![]() 的长.
的长.
∵∠ABC=45°,∴∠BCF′=67.5°,∴∠BOF′=135°,∴![]() 的长为
的长为![]() =
=![]() .
.


练习册系列答案
相关题目