题目内容
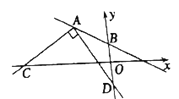
【题目】如图,在平面直角坐标系中,点A的坐标为(﹣4,4),点B的坐标为(0,2).
(1)求直线AB的解析式;
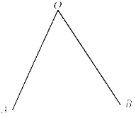
(2)如图,以点A为直角顶点作∠CAD=90°,射线AC交x轴于点C,射线AD交y轴于点D.当∠CAD绕着点A旋转,且点C在x轴的负半轴上,点D在y轴的负半轴上时,OC﹣OD的值是否发生变化?若不变,求出它的值;若变化,求出它的变化范围.
【答案】(1)![]() ;(2)不变,值为8.
;(2)不变,值为8.
【解析】
(1)由![]() 、
、![]() 两点的坐标利用待定系数法可求得直线
两点的坐标利用待定系数法可求得直线![]() 的解析式;
的解析式;
(2)过![]() 分别作
分别作![]() 轴和
轴和![]() 轴的垂线,垂足分别为
轴的垂线,垂足分别为![]() 、
、![]() ,可证明
,可证明![]() ,可得到
,可得到![]() ,从而可把
,从而可把![]() 转化为
转化为![]() ,再利用线段的和差可求得
,再利用线段的和差可求得![]()
![]()
![]() .
.
解:(1)设直线![]() 的解析式为:
的解析式为:![]() .
.
![]() 点
点![]() ,点
,点![]() 在直线
在直线![]() 上,
上,
![]()
![]() ,
,
解得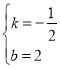 .
.
![]() 直线
直线![]() 的解析式为:
的解析式为:![]() ;
;
(2)不变.
理由如下:
过点![]() 分别作
分别作![]() 轴、
轴、![]() 轴的垂线,垂足分别为
轴的垂线,垂足分别为![]() 、
、![]() ,如图1.
,如图1.
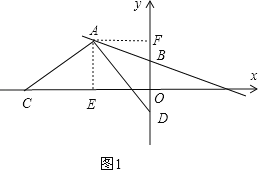
则![]() ,
,
又![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() .
.
![]() ,
,
![]() .
.
在![]() 和
和![]() 中,
中,
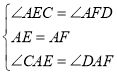 ,
,
![]() ,
,
![]() .
.
![]() .
.
故![]() 的值不发生变化,值为8.
的值不发生变化,值为8.

练习册系列答案
 夺冠金卷全能练考系列答案
夺冠金卷全能练考系列答案
相关题目