题目内容
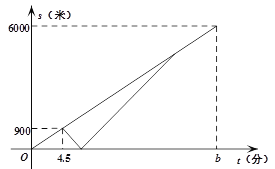
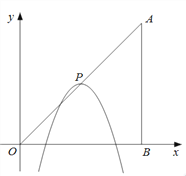
【题目】如图,在平面直角坐标系中,点A、B的坐标分别为(6,6)、(6,0).抛物线![]() 的顶点P在折线OAAB上运动.
的顶点P在折线OAAB上运动.
(1)当点P在线段OA上运动时,抛物线![]() 与y轴交点坐标为(0,c).
与y轴交点坐标为(0,c).
①用含m的代数式表示n;
②求c的取值范围;
(2)当抛物线![]() 经过点B时,求抛物线所对应的函数表达式.
经过点B时,求抛物线所对应的函数表达式.
【答案】(1)①![]() ;②-30≤c≤
;②-30≤c≤![]() ;(2)
;(2)![]() 或一般式(
或一般式(![]() ).
).
【解析】试题分析:(1)待定系数法求出OA直线,再求出二次函数顶点坐标的关系,求范围.(2) 当点P在线段OA上或者线段AB上时,分别讨论,求出二次函数表达式.
试题解析:
(1)①设直线OA所对应的函数表达为y=kx.
∵A(6,6)
∴![]() , ∴
, ∴![]() , ∴
, ∴![]() .
.
∵y=-(x-m)2+n的顶点P在OA上,
∴![]() .
.
②由题意得:,y=-x2+2mx-m2+m.
∵抛物线与![]() 轴交点坐标为(0,
轴交点坐标为(0, ![]() ),
),
![]() .
.
∵点P在线段OA上,
∴0≤![]() ≤6.
≤6.
![]() ,
,
∵0<![]() <6,
<6,
∴当![]() .
.
当![]() .
.
∴c的取值范围为-30≤c≤![]() .
.
(2)当点P在线段OA上时,
∵抛物线经过B(6,0),
∴-(6-m)2+m=0,
∴.m1=4,m2=9,
∴ y=-(x-4)2+4或一般式(y=-x2+8x-12).
当点P在线段AB上时,
点P与点B重合,
∴m=6.
∴ y=-(x-6)2或一般式(y=-x2+12x-36).

练习册系列答案
 好成绩1加1期末冲刺100分系列答案
好成绩1加1期末冲刺100分系列答案 金状元绩优好卷系列答案
金状元绩优好卷系列答案
相关题目
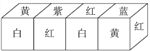
【题目】把正方体的六个面分别涂上六种不同的颜色,并画上朵数不等的花,各面上的颜色与花的朵数情况见下表:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
现将上述大小相同,颜色、花朵分布也完全相同的四个正方体拼成一个水平放置的长方体,如图所示.问:长方体的下底面共有多少朵花?