��Ŀ����
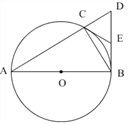
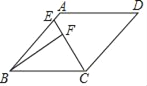
����Ŀ��������ȫ�ȵĵ���ֱ�����ǰ�ABC��EFG(��ֱ�DZ߳���Ϊ4)������һ��(��ͼ1)����ʹ���ǰ�EFG��ֱ�Ƕ���G�����ǰ�ABC��б���е�O�غϣ��ֽ����ǰ�EFG��O��˳ʱ����ת����ת��![]() ��������
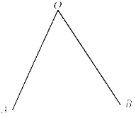
��������![]() �ı���CHGK����ת�����������ǰ���ص�����(��ͼ2).
�ı���CHGK����ת�����������ǰ���ص�����(��ͼ2).
(1)��������ת�����У�BH��CK��������������ϵ��֤����Ľ��ۣ�
(2)��������ת�����У�����ֱ�������ε��ص���������Ƿ�ᷢ���ı䣿֤����Ľ���.

���𰸡�������
��������
�������������֤��������CGK��������BGHȫ�ȣ��Ӷ��ó����ǵ������ȣ��������ı���CHGK�����ת����������CGB�����Ҳ����������ABC�����һ�룬�ɴ˿ɵó��ı���CHGK�������4�����Բ���ı�.
���������BH=CK.�ı���CHGK�����û�б仯.�ߡ�ABC�ǵ���ֱ��������,OΪб���е�,
��CG=BG,CG��AB,���ACG=��B=45��,�ߡ�BGH����CGK��Ϊ��ת��,���BGH=��CGK,
�����CGK���Կ���������BGH�Ƶ�O˳ʱ����ת����,��BH=CK,S��CGK=S��BGH,
��S�ı���CHGK=S��CGK+S��CGH=S��BGH+S��CGH=S��BCG=![]() S��ABC=
S��ABC=![]() ��
��![]() ��4��4=4.
��4��4=4.
���ı���CHGK���������ת������û�б仯,ʼ��Ϊ4.