题目内容
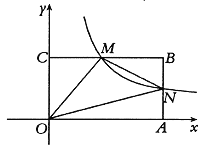
【题目】如图,一次函数y=x﹣2与反比例函数y=![]() (x>0)的图象相交于点M(m,1).
(x>0)的图象相交于点M(m,1).
(1)填空:m的值为 ,反比例函数的解析式为 ;
(2)已知点N(n,n),过点N作l1∥x轴,交直线y=x﹣2于点A,过点N作l2∥y轴,交反比例函数y=![]() (x>0)的图象与点B,试用n表示△NAB的面积S.
(x>0)的图象与点B,试用n表示△NAB的面积S.
【答案】(1)3,y=![]() ;(2)|
;(2)|![]() ﹣n|.
﹣n|.
【解析】分析:(1)把M(m,1)代入一次函数y=x-2,可得m的值;把M(3,1)代入反比例函数y=![]() (x>0),可得k的值;
(x>0),可得k的值;
(2)依据点N与点A的纵坐标相同,均为n,可得AN=n+2-n=2,依据点N与点B的横坐标相同,均为n,可得BN=|![]() -n|,即可得到S△NBA=
-n|,即可得到S△NBA=![]() ×2×|
×2×|![]() -n|=|
-n|=|![]() -n|.
-n|.
详解:(1)把M(m,1)代入一次函数y=x-2,可得
1=m-2,
解得m=3,
把M(3,1)代入反比例函数y=![]() (x>0),可得
(x>0),可得
k=3×1=3,
∴反比例函数的解析式为y=![]() ,
,
(2)由题可得,点N与点A的纵坐标相同,均为n,
将y=n代入y=x-2中,得x=n+2,
∴A(n+2,n),
∴AN=n+2-n=2,
由题可得,点N与点B的横坐标相同,均为n,
将x=n代入y=![]() 中,得y=
中,得y=![]() ,
,
∴B(n,![]() ),
),
∴BN=|![]() -n|,
-n|,
∴S△NBA=![]() ×2×|
×2×|![]() -n|=|
-n|=|![]() -n|.
-n|.


练习册系列答案
 励耘书业暑假衔接宁波出版社系列答案
励耘书业暑假衔接宁波出版社系列答案
相关题目