题目内容
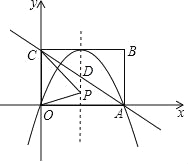
【题目】如图,在平面直角坐标系中,直线y=-3x+3与x轴、y轴分别交于A、B两点,以AB为边在第一象限作正方形ABCD,顶点D恰好落在双曲线y=![]() .若将正方形沿x轴向左平移b个单位长度后,点C恰好落在该双曲线上,则b的值为( )
.若将正方形沿x轴向左平移b个单位长度后,点C恰好落在该双曲线上,则b的值为( )

A. 1 B. 2 C. 3 D. 4
【答案】B
【解析】
作DE⊥x轴于E,CF⊥y轴于F,如图,先根据坐标轴上点的坐标特征得到B(0,3),A(1,0),再证明△AOB≌△DEA得到AE=OB=3,DE=OA=1,则D(4,1),同样方法可得C(3,4),接着根据反比例函数图象上点的坐标特征确定k=4,则反比例函数解析式为y=![]() ,然后计算当y=4时所对应的自变量,从而可确定b的值.
,然后计算当y=4时所对应的自变量,从而可确定b的值.
作DE⊥x轴于E,CF⊥y轴于F,如图,当x=0时,y=﹣3x+3=3,则B(0,3);当y=0时,﹣3x+3=0,解得:x=1,则A(1,0).
∵四边形ABCD为正方形,∴AB=AD,∠BAD=90°,∴∠2+∠3=90°,而∠1+∠2=90°,∴∠1=∠3.
在△AOB和△DEA中,∵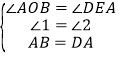 ,∴△AOB≌△DEA,∴AE=OB=3,DE=OA=1,∴D(4,1),同样方法可得△AOB≌△BFC,∴CF=OB=3,BF=OA=1,∴C(3,4),而顶点D(4,1)落在双曲线y=
,∴△AOB≌△DEA,∴AE=OB=3,DE=OA=1,∴D(4,1),同样方法可得△AOB≌△BFC,∴CF=OB=3,BF=OA=1,∴C(3,4),而顶点D(4,1)落在双曲线y=![]() 上,∴k=4×1=4,∴反比例函数解析式为y=
上,∴k=4×1=4,∴反比例函数解析式为y=![]() ,当y=4时,
,当y=4时,![]() =4,解得:x=1,∴C点向左平移2个单位恰好落在该双曲线上,即b=2.
=4,解得:x=1,∴C点向左平移2个单位恰好落在该双曲线上,即b=2.
故选B.

练习册系列答案
 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案 名题训练系列答案
名题训练系列答案
相关题目