Question

【题目】已知，直线AB∥CD.

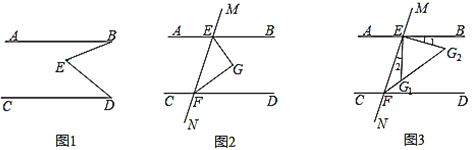
(1)如图1，若点E是AB、CD之间的一点，连接BE.DE得到∠BED．求证：∠BED＝∠B+∠D.

(2)若直线MN分别与AB、CD交于点E.F．

①如图2，∠BEF和∠EFD的平分线交于点G．猜想∠G的度数，并证明你的猜想；

②如图3，EG1和EG2为∠BEF内满足∠1＝∠2的两条线，分别与∠EFD的平分线交于点G1和G2．求证：∠FG1E+∠G2＝180°．

Answer 1

【答案】(1)证明见解析；(2)①∠EGF＝90°，证明见解析；②证明见解析.

【解析】

（1）过点E作EF∥AB，则有∠BEF=∠B根据平行线的性质即可得到结论；
（2）①由（1）中的结论得∠EGF=∠BEG+∠GFD，根据EG、FG分别平分∠BEF和∠EFD，得到∠BEF=2∠BEG，∠EFD=2∠GFD，由于BE∥CF到∠BEF+∠EFD=180°，于是得到2∠BEG+2∠GFD=180°，即可得到结论；
②过点G1作G1H∥AB，由结论可得∠G2=∠1+∠3，由平行线的性质得到∠3=∠G2FD，由于FG2平分∠EFD，求得∠EFG2=∠G2FD=∠3，由于∠1=∠2，于是得到∠G2=∠2+∠EFG2，由三角形外角的性质得到∠EG1G2＝∠2+∠EFG2=∠G2，然后根据平角的性质即可得到结论．

（1）证明：如图1过点E作EF∥AB，则有∠BEF＝∠B．

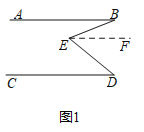
∵AB∥CD，

∴EF∥CD．

∴∠FED＝∠D．

∴∠BEF+∠FED＝∠B+∠D．

即∠BED＝∠B+∠D；

（2）①如图2所示，猜想：∠EGF＝90°.

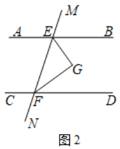
证明：由(1)中的结论得∠EGF＝∠BEG+∠GFD，

∵EG.FG分别平分∠BEF和∠EFD，

∴∠BEF＝2∠BEG，∠EFD＝2∠GFD，

∵BE∥CF，

∴∠BEF+∠EFD＝180°，

∴2∠BEG+2∠GFD＝180°，

∴∠BEG+∠GFD＝90°，

∵∠EGF＝∠BEG+∠GFD，

∴∠EGF＝90°；

②证明：如图3，过点G1作G1H∥AB

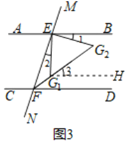
∵AB∥CD

∴G1H∥CD

∴∠3＝∠G2FD

由（1）结论可得∠G2＝∠1+∠3

∵FG2平分∠EFD

∴∠EFG2＝∠G2FD=∠3

∵∠1＝∠2

∴∠G2＝∠2+∠EFG2

∵∠EG1G2＝∠2+∠EFG2

∴∠G2＝∠EG1G2

∵∠FG1E+∠EG1G2＝180°

∴∠FG1E+∠G2＝180°．