题目内容
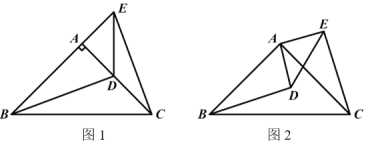
【题目】如图,已知等腰直角三角形ABC,点P是斜边BC上一点(不与B,C重合),PE是△ABP的外接圆⊙O的直径.
(1)求证:△APE是等腰直角三角形;
(2)若⊙O的直径为2,求![]() 的值.
的值.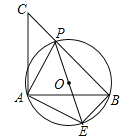
【答案】(1)证明见解析;(2)4.
【解析】试题分析:(1)根据等腰直角三角形性质得出∠C=∠ABC=∠PEA=45°,再由PE是⊙O的直径,得出∠PAE=90°,∠PEA=∠APE=45°,从而得证.
(2)根据题意可知,AC=AB,AP=AE,再证△CPA≌△BAE,得出CP=BE,依勾股定理即可得证.
试题解析:(1)证明:∵△ABC是等腰直角三角形,
∴∠C=∠ABC=45°,
∴∠PEA=∠ABC=45°
又∵PE是⊙O的直径,
∴∠PAE=90°,
∴∠PEA=∠APE=45°,
∴△APE是等腰直角三角形.
(2)∵△ABC是等腰直角三角形,
∴AC=AB,
同理AP=AE,
又∵∠CAB=∠PAE=90°,
∴∠CAP=∠BAE,
∴△CPA≌△BAE,
∴CP=BE,
在Rt△BPE中,∠PBE=90°,PE=2,
∴PB2+BE2=PE2,
∴CP2+PB2=PE2="4."

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
【题目】某校要从新入学的两名体育特长生李勇、张浩中挑选一人参加校际跳远比赛,在跳远专项测试以及以后的![]() 次跳远选拔赛中,他们的成绩(单位:
次跳远选拔赛中,他们的成绩(单位:![]() )如下表所示:
)如下表所示:
专项测试和 | 平均数 | 方差 | |||||||
李勇 |
|
|
|
|
|
|
|
| |
张浩 |
|
|
|
|
|
|
|
| |
![]() 求张浩同学
求张浩同学![]() 次测试成绩的平均数,李勇同学
次测试成绩的平均数,李勇同学![]() 次测试成绩的方差;
次测试成绩的方差;
![]() 请你分别从平均数和方差的角度分析两人成绩的特点;
请你分别从平均数和方差的角度分析两人成绩的特点;
![]() 经查阅历届比赛的资料,成绩若达到
经查阅历届比赛的资料,成绩若达到![]() ,就很可能得到冠军,你认为应选谁去参赛夺冠军比较有把握?说明理由;
,就很可能得到冠军,你认为应选谁去参赛夺冠军比较有把握?说明理由;
![]() 以往的该项最好成绩的纪录是
以往的该项最好成绩的纪录是![]() ,若要想打破纪录,你认为应选谁去参赛?
,若要想打破纪录,你认为应选谁去参赛?