题目内容
【题目】材料：数学兴趣一小组的同学对完全平方公式进行研究：因
，将左边展开得到
，移项可得：
.
数学兴趣二小组受兴趣一小组的启示，继续研究发现：对于任意两个非负数
、
，都存在
，并进一步发现，两个非负数、的和一定存在着一个最小值.
根据材料，解答下列问题：
（1）
__________（
，
）；
___________（）；
（2）求
的最小值；
（3）已知
，当
为何值时，代数式
有最小值，并求出这个最小值.
【答案】（1）
，2；（2）
；（3）当
时，代数式
的最小值为2019.
【解析】
（1）根据阅读材料即可得出结论；
（2）根据阅读材料介绍的方法即可得出结论；
（3）把已知代数式变为
，再利用阅读材料介绍的方法，即可得到结论．
（1）∵
，
，
∴
，
∵，
∴
；
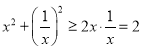（2）当x
时，
，
均为正数，
∴
所以，
的最小值为．
（3）当x
时，，
，2x-6均为正数，
∴
由
可知，当且仅当
时，
取最小值，
∴当
，即时，有最小值．
∵x
故当时，代数式的最小值为2019．
练习册系列答案
相关题目
【题目】为提醒人们节约用水，及时修好漏水的水龙头．小明同学做了水龙头漏水实验，每隔10秒观察量筒中水的体积，记录的数据如表（漏出的水量精确到1毫升），已知用于接水的量筒最大容量为100毫升．
时间t（秒） | 10 | 20 | 30 | 40 | 50 | 60 | 70 |
量筒内水量v（毫升） | 4 | 6 | 8 | 10 | 12 | 14 | 16 |
（1）在图中的平面直角坐标系中，以（t,v）为坐标描出上表中数据对应的点；
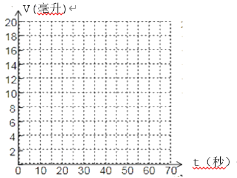
（2）用光滑的曲线连接各点，你猜测V与t的函数关系式是______________．
（3）解决问题：
①小明同学所用量筒开始实验前原有存水 毫升；
②如果小明同学继续实验，当量筒中的水刚好盛满时，所需时间是_____秒；
③按此漏水速度，半小时会漏水 毫升．
