Question

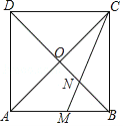
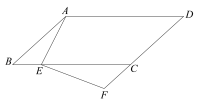
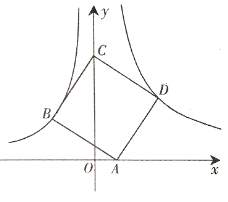
【题目】如图，正方形 ABCD 的顶点 A 在 x 轴的正半轴上，顶点 C 在 y 轴的正半轴上，点 B 在双曲线 y ( x 0) 上，点 D 在双曲线 y ( x 0) 上，点 D 的坐标是 （3，3）.

（1）求 k 的值

（2）求点 A 和点 C 的坐标

Answer 1

【答案】（1）9；（2），.

【解析】

（1）将点D的坐标代入双曲线即可得；

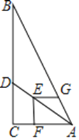
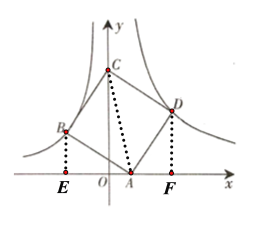
（2）如图（见解析），过B作BE垂直x轴于点E，过点D作DF垂直x轴于点F，连接AC；设点B的坐标为，则，根据三角形全等的判定定理易证，由三角形全等的性质得，结合点D的坐标可求出的值，则可求出点A的坐标，也可求出正方形ABCD的边长，进而求出对角线AC的长，最后在中，利用勾股定理求得OC的长，即可得出点C的坐标.

（1）点在双曲线上

代入得，解得

故的值为9；

（2）如图，过B作BE垂直x轴于点E，过点D作DF垂直x轴于点F，连接AC

设点B的坐标为，则

四边形ABCE为正方形

又

在和中，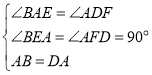

根据点D的坐标可得：

解得：

又点B在双曲线上，则

联立可得：

则，故点A的坐标为

在中，

由勾股定理得：

在中，由勾股定理得：

故点C的坐标为

综上，点A的坐标为，点C的坐标为.