题目内容
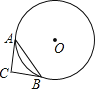
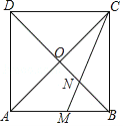
【题目】如图,正方形ABCD的对角线AC与BD相交于点O,∠ACB的平分线分别交AB、BD于M、N两点.若AM=![]() ,则线段BN的长为( )
,则线段BN的长为( )
A.1B.![]() C.2
C.2![]() D.
D.![]()
【答案】A
【解析】
作MH⊥AC于H,根据CM平分∠ACB与正方形的性质可证∠BNM=∠BMN,即可得出BN=BM=1.
作MH⊥AC于H,如图,

∵四边形ABCD为正方形,
∴∠MAH=45°,
∴△AMH为等腰直角三角形,
∵AM=![]() ,
,
∴AH=MH=1,
∵CM平分∠ACB,∠ACB=45°,∠MBC=90°
∴∠ACM=∠BCM=22.5°,BM=MH=1,
∵∠BAC=45°,
∴∠BMC=45°+22.5°=67.5°,
∵∠BNM=∠ONC=90°–22.5°=67.5°,
∴∠BNM=∠BMN,
∴BN=BM=1,故选A.

练习册系列答案
 学练快车道快乐假期暑假作业新疆人民出版社系列答案
学练快车道快乐假期暑假作业新疆人民出版社系列答案 浙大优学小学年级衔接导与练浙江大学出版社系列答案
浙大优学小学年级衔接导与练浙江大学出版社系列答案 小学暑假作业东南大学出版社系列答案
小学暑假作业东南大学出版社系列答案 津桥教育暑假拔高衔接广东人民出版社系列答案
津桥教育暑假拔高衔接广东人民出版社系列答案 波波熊暑假作业江西人民出版社系列答案
波波熊暑假作业江西人民出版社系列答案
相关题目
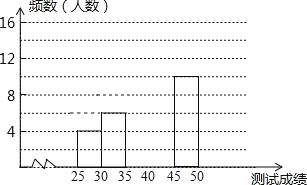
【题目】为了提高学生书写汉字的能力.增强保护汉字的意识,我区举办了“汉字听写大赛”,经选拔后有50名学生参加决赛,这50名学生同时听写50个汉字,若每正确听写出一个汉字得1分,根据测试成绩绘制出部分频数分布表和部分频数分布直方图如图表:
组别 | 成绩x分 | 频数(人数) |
第1组 | 25≤x<30 | 4 |
第2组 | 30≤x<35 | 6 |
第3组 | 35≤x<40 | 14 |
第4组 | 40≤x<45 | a |
第5组 | 45≤x<50 | 10 |
请结合图表完成下列各题:
(1)求表中a的值;
(2)请把频数分布直方图补充完整;
(3)若测试成绩不低于40分为优秀,则本次测试的优秀率是多少?
(4)第5组10名同学中,有4名男生,现将这10名同学平均分成两组进行对抗练习,且4名男同学每组分两人,试用列表法或画树状图的方法求小宇和小强两名男同学能分在一组的概率.