Question

【题目】如图，在矩形ABCD中，AB＝3，BC＝5，点E在AD边上且不与点A和点D重合，点O是对角线BD的中点，当△OED是等腰三角形时，AE的长为_____．

Answer 1

【答案】或5﹣．

【解析】

分三种情况讨论：①当OE＝DE时，△OED是等腰三角形，连接OA，根据勾股定理可求BD，根据点O是中点可知OD＝OB＝OA，进而可证得△ODE∽△ADO，得到相似比即可求出答案；②DE＝OD，继而可知AE=AD-OD；③OD＝OEE与点A重合，不合题意舍去，故此可得出最终答案.

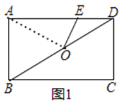
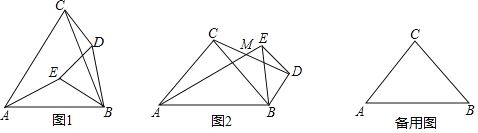
①当OE＝DE时，△OED是等腰三角形，如图1，连接OA，在矩形ABCD中，CD＝AB＝3，AD＝BC＝5，∠BAD＝90°，

在Rt△ABD中，根据勾股定理得，BD＝，

∵O是BD中点，

∴OD＝OB＝OA＝，

∴∠OAD＝∠ODA，

∵OE＝DE，

∴∠EOD＝∠ODE，

∴∠EOD＝∠ODE＝∠OAD，

∴△ODE∽△ADO，

∴，∴DO2＝DEDA，

∴设AE＝x，

∴DE＝5﹣x，

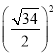∴＝5（5﹣x），

∴x＝，

即：AE＝；

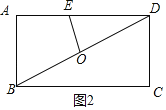
②如图2，当DE＝OD＝时，当△OED是等腰三角形，

∴AE＝5﹣；

③当OD＝OE＝时，当E与点A重合，不合题意舍去，

综上所述，当△OED是等腰三角形时，AE的长为或5﹣；

故答案为：或5-．