Question

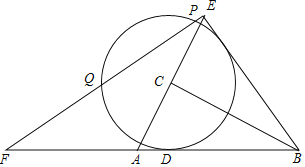
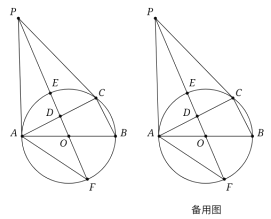
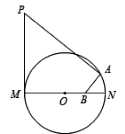
【题目】如图，MN为⊙OD的直径，PM为⊙O的切线，PM=MN=4，点A在⊙O上，AB⊥PA交MN于B．若B为ON的中点，则AB的长为（ ）

A.B.C.D.

Answer 1

【答案】B

【解析】

连接AM,PB,AN,则PB=5，设AB=a，再证明△PAM∽△ABN，最后用勾股定理解答即可．

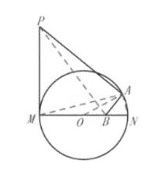
解：如图：连接AM,PB,AN,则∠MAN=90°

由题意可得：PM=4,MB=3,BN=1

∴PB=

∵PM为⊙O的切线

∴PM⊥MN

又∵∠MAN=90°

∴∠PMA+∠AMB=∠ANM+∠AMB

∴∠PMA =∠ANM

又∵∠MAN=90°, AB⊥PA

∴∠MAP+∠MAB=∠ANB+∠BAN

∴∠MAP =∠NAB

∴△PAM∽△ABN

∴

设AB=a,则,即AP=4a

在Rt△PBA中,有PA2+AB2=PB2,解得:AB=．

故答案为B．