Question

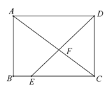
【题目】如图，⊙O是△ABC的外接圆，AB是直径，D是AC中点，直线OD与⊙O相交于E，F两点，P是⊙O外一点，P在直线OD上，连接PA，PC，AF，且满足∠PCA＝∠ABC．

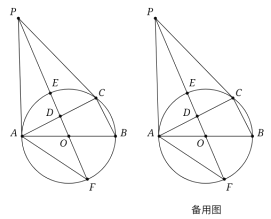
（1）证明：EF2＝4ODOP；

（2）若tan∠AFP＝，求的值．

Answer 1

【答案】(1)证明见解析；(2) ．

【解析】

（1）由D是AC中点可得OD⊥AC,则PA=PC;设∠PAD=∠1，∠PCD=∠2，∠BAC=∠3，可得∠1=∠2；又∠2=∠B,AB是直径，则∠ACB=90°，进一步说明∠PAB=90°；再由摄影定理可得：△AOD∽△POA，得即 ,再根据AO=EF,即可完成证明；

（2）由tan∠AFP＝，设AD=2，DF=3，则A0=OF=x,OD=3-x ,AD2+DO2=A02，可求x= ，进一步即可完成解答．

解：（1）∵D是AC中点，

∴OD⊥AC，

∴PA=PC

设∠PAD=∠1，∠PCD=∠2，∠BAC=∠3

∴∠1=∠2，

∵∠2=∠B,AB是直径

∴∠ACB=90°，∠B+∠3=90°

∴∠1+∠3=90°，

∴∠PAB=90°

根据射影定理可得△AOD∽△POA

∴即

∵AO=EF，

∴EF2＝4ODOP；

(2) 由tan∠AFP＝，设AD=2，DF=3，则A0=OF=x,OD=3-x ,

∴AD2+DO2=A02即22+(3-x)2=x2，求得x=，

∴DO=

∵AO=BO,AD=CD，

∴OD=BC，

∴BC=2DO=

∵DE=OE-OD=

∴=．