Question

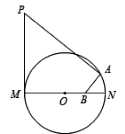
【题目】如图，Rt△ABC中，∠ACB＝90°，AC＝6，AB＝10，⊙C与AB相切于点D，延长AC到点E，使CE＝AC，连接EB．过点E作BE的垂线，交⊙C于点P、Q，交BA的延长线于点F．

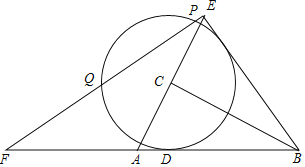
（1）求AD的长；

（2）求证：EB与⊙C相切；

（3）求线段PQ的长．

Answer 1

【答案】（1）；（2）见解析；（3）

【解析】

（1）连结CD，易证△ACD∽△ABC，由相似三角形的性质即可求得AD的长；

（2）过点C作CK⊥BE交BE于点K，要证EB与⊙C相切，即证CK=CD=圆的半径，由∠ACB=90°且CE=AC可证得BE是∠ABE的平分线，即可证得CK=CD；

（3）过点C作CG⊥FE交FE于点G，由矩形的性质和全等三角形的性质得CG=AD，由勾股定理可求得GQ，即可求出PQ．

解：（1）如图，连接CD，

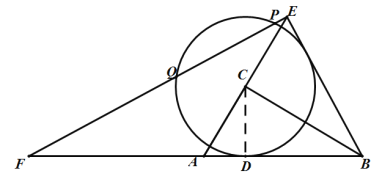
∵⊙C与AB相切于点D，

∴CD⊥AB，则∠ADC=90°，

∴∠CAD+∠ACD=90°，

∵∠ACB=90°，

∴∠CAD+∠CBA=90°，∠ADC=∠ACB=90°，

∴∠ACD=∠CBA，

∴△ACD∽△ABC，

∴，

∵AC=6，AB=10，

∴，

∴AD=；

（2）如图，过点C作CK⊥BE交BE于点K，

∵∠ACB=90°，CE=AC，即BC垂直且平分AE，

∴BA=BE，△BAE是等腰三角形，

∴BC平分∠ABE，

∵CD⊥AB，CK⊥BE，

∴CK=CD=圆的半径，

∴EB与⊙C相切；

（3）如图，过点C作CG⊥FE交FE于点G，连结CQ，

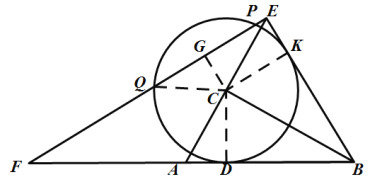
∴PQ=2QG，∠CGE=90°，

又∵EF⊥BE，CK⊥BE，

∴∠GEK=∠CKE=∠CGE=90°，

∴四边形EGCF为矩形，

∴GE=CK，

由（2）可知CK=CD，

∴GE=CD，

在Rt△ADC和Rt△CGE中，

∴Rt△ADC≌Rt△CGE，

∴CG=AD=，

∵AC=6，AD=，

∴，

∴CQ=CD=，

∴，

∴PQ=2GQ=．