Question

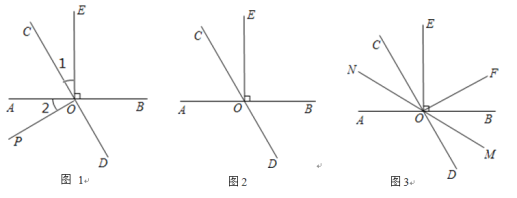
【题目】已知：直线 AB与直线 CD交于点 O，过点 O作 OE⊥AB．

①如图 1，OP 为∠AOD 内的一条射线，若∠1＝∠2，求证：OP⊥CD；

②如图 2，若∠BOC＝2∠AOC，求∠COE 的度数；

③如图 3．在（2）的条件下，过点 O 作 OF⊥CD，经过点 O 画直线 MN，若射线 OM平分∠BOD，请直接写出图中与 2∠EOF 度数相等的角．

Answer 1

【答案】①见解析；②∠COE=；③∠AOD、∠BOC、∠FON、∠EOM

【解析】

①直接根据等量代换即可证明.

②先根据平角的定义可得∠AOC=，再利用垂直的定义可得∠AOE=，从而得出结论.

③根据②中∠AOC=，分别计算各角的度数，得其中∠EOF=，根据各角的度数可得结论.

解：①∵OE⊥AB

∴∠AOC+∠1=

∵∠1＝∠2

∴∠AOC+∠2=

∴OP⊥CD

②∵∠AOC+∠BOC=，且∠BOC＝2∠AOC

∴∠AOC=

∵OE⊥AB

∴∠AOE=

∴∠COE=-=

③由②知：∠AOC=

∵射线 OM平分∠BOD

∴∠BOM=∠DOM=∠AON=∠CON=

∵OE⊥AB,OC⊥OF

∴∠AOE=∠COF=

∴∠AOC=∠EOF=

∴∠AOD=∠BOC=∠FON=∠EOM==2∠EOF

∴与2∠EOF度数相等的角是：∠AOD、∠BOC、∠FON、∠EOM.