题目内容
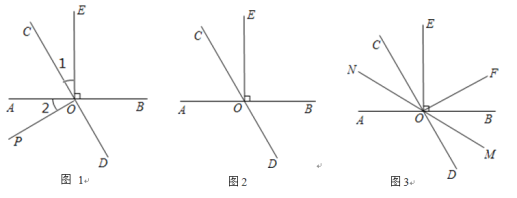
【题目】(1)请用两种不同的方法列代数式表示图1中阴影部分的面积.

方法①: ;
方法②: ;
(2)根据(1)写出一个等式: ;
(3)若x+y=8,xy=3.75,利用(2)中的结论,求x,y;
(4)有许多代数恒等式可以用图形的面积来表示.如图2,它表示了(2m+n)(m+n)=2m2+3mn+n2.试画出一个几何图形,使它的面积能表示(2m+n)(m+2n)=2m2+5mn+2n2.
【答案】(1)(m+n)2﹣4mn;(m﹣n)2;(2)(m+n)2﹣4mn=(m﹣n)2;(3)![]() 或
或![]() ;(4)见解析.
;(4)见解析.
【解析】
(1)第一种方法为:大正方形面积﹣4个小长方形面积,第二种表示方法为:阴影部分为小正方形的面积;
(2)依据大正方形面积﹣4个小长方形面积=阴影部分为小正方形的面积,即可得到等式;
(3)利用(x﹣y)2=(x+y)2﹣4xy,再求x﹣y,即可解答;
(4)根据多项式画出长方形,即可解答.
解:(1)方法①:(m+n)2﹣4mn,
方法②:(m﹣n)2;
故答案为:(m+n)2﹣4mn,(m﹣n)2;
(2)由①可得:(m+n)2﹣4mn=(m﹣n)2;
故答案为:(m+n)2﹣4mn=(m﹣n)2;
(3)由②可得:(x﹣y)2=(x+y)2﹣4xy,
∵x+y=﹣8,xy=3.75,
∴(x﹣y)2=64﹣15=49,
∴x﹣y=±7;
又∵x+y=8,
∴![]() 或
或![]() ;
;
(4)如图,表示(2m+n)(m+2n)=2m2+5mn+2n2:

【题目】为了帮助本市一名患“白血病”的高中生,某班15名同学积极捐款,他们捐款数额如下表:
捐款的数额(单位:元) | 5 | 10 | 20 | 50 | 100 |
人数(单位:个) | 2 | 4 | 5 | 3 | 1 |
关于这15名同学所捐款的数额,下列说法正确的是
A.众数是100 B.平均数是30 C.极差是20 D.中位数是20
【题目】在我校“书香校园”活动中,某数学小组为了解学生家庭藏书情况,随机抽取我校部分学生进行调查,并绘制成部分统计图如下表:
类别 | 家庭藏书情况统计表 | 学生人数 |
|
| 20 |
|
|
|
|
| 50 |
|
| 66 |
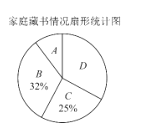
根据以上信息,解答下列问题:
(1)参加调查的学生人数为多少,a等于多少,本次调查结果的中位数在哪一类.
(2)在扇形统计图中,“![]() ”对应扇形的圆心角为多少.
”对应扇形的圆心角为多少.
(3)若我校有4500名学生,请估计全校学生中藏书200本以上的人数.
【题目】某校为了解学生的每周平均课外阅读时间,在本校随机抽取若干名学生进行调查,并将调查结果绘制成如下不完整的统计图表,请根据图表中所给的信息,解答下列问题:
组别 | 阅读时间t(单位:小时) | 频数(人数) |
A | 0≤t<1 | 8 |
B | 1≤t<2 | 20 |
C | 2≤t<3 | 24 |
D | 3≤t<4 | m |
E | 4≤t<5 | 8 |
F | t≥5 | 4 |
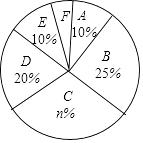
(1)图表中的m= , n=;
(2)扇形统计图中F组所对应的圆心角为度;
(3)该校共有学生1500名,请估计该校有多少名学生的每周平均课外阅读时间不低于3小时?