题目内容
【题目】如图，点E是正方形ABCD的边DC上一点，把△ADE顺时针旋转△ABF的位置．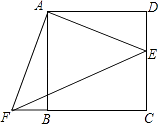
（1）旋转中心是点 ， 旋转角度是度；
（2）若连结EF，则△AEF是三角形；并证明；
（3）若四边形AECF的面积为25，DE=2，求AE的长．
【答案】
（1）A；90
（2）等腰直角
（3）
解：由题意得：△ADE≌△ABF，
∴S四边形AECF=S正方形ABCD=25，
∴AD=5，而∠D=90°，DE=2，
∴ 
．
【解析】 解：（1）如图，由题意得：旋转中心是点A，旋转角度是90度．故答案为A、90．（2）由题意得：AF=AE，∠EAF=90°，∴△AEF为等腰直角三角形．故答案为等腰直角．
（1）根据旋转变换的定义，即可解决问题．（2）根据旋转变换的定义，即可解决问题．（3）根据旋转变换的定义得到△ADE≌△ABF，进而得到S四边形AECF=S正方形ABCD=25，求出AD的长度，即可解决问题．
练习册系列答案
相关题目
