题目内容
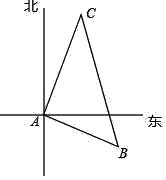
【题目】如图,在平面直角坐标系中,A(a,b),B(c,0),|a-3|+(2b-c)2+![]() =0.
=0.

(1)求点A,B的坐标;
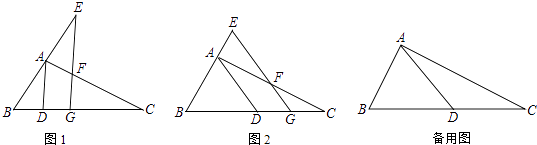
(2)如图,点C为x轴正半轴上一点,且OC=OA,点D为OC的中点,连AC,AD,请探索AD+CD与![]() AC之间的大小关系,并说明理由;
AC之间的大小关系,并说明理由;

(3)如图,过点A作AE⊥y轴于E,F为x轴负半轴上一动点( 不与(-3,0)重合 ),G在EF延长线上,以EG为一边作∠GEN=45°,过A作AM⊥x轴,交EN于点M,连FM,当点F在x轴负半轴上移动时,式子![]() 的值是否发生变化?若变化,求出变化的范围;若不变化,请求出其值并说明理由.
的值是否发生变化?若变化,求出变化的范围;若不变化,请求出其值并说明理由.

【答案】(1)A(3,3),B(6,0);(2)AD+CD>![]() AC;(3)不变化,1.
AC;(3)不变化,1.
【解析】
(1)利用非负性建立方程即可得出结论;
(2)延长AD到E,使DE=AD,连接OE,先证明△ACD≌△EOD, 得到AC=OE, 再依据三角形的三边关系即可得出结论;
(3)在AM上截取AN=OF,连EH,易证△AEH≌△OEF,再根据角与角之间的关系,证明△MEH≌△MEF,则有FM=HM,即可求得该式子的值.
解:(1)∵|a-3|+(2b-c)2+![]() =0,
=0,
∴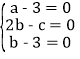 ,解得
,解得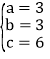 ,
,
∴A(3,3),B(6,0).
(2)延长AD到E,使DE=AD,连接OE,则AE=2AD,
∵AD为△ABC的中线
∴OD=CD
在△ACD和△EOD中
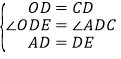 ,
,
∴△ACD≌△EOD
∴AC=OE
在△AOE中,根据三角形的三边关系有
AO+OE>>AE
而OC=OA,AE=2AD
∴2CD+2AD>AC
即AD+CD>![]() AC;
AC;
(3)不变,
在AM上截取AH=OF,连接EH,
∵A(3,3),
∴OE=AE,
∵∠A=∠EOF=90°,AH=OF,
∴△AEH≌△OEF(SAS),
∴EH=EF,∠AEH=∠FEO,
∵∠AEO=90°,
∴∠HEM=90°-∠AEH-∠MEO=90°-45°=45°,
∴∠NEH=∠MEF=45°,
∵EM=EM,
∴△MEH≌△MEF(SAS),
∴FM=HM,
∴![]() =
= ![]() =
= ![]() = 1.
= 1.

 阅读快车系列答案
阅读快车系列答案