题目内容
【题目】在平面直角坐标系中,点A![]() 点B
点B![]() 已知
已知![]() 满足
满足![]() .
.
(1)点A的坐标为_________,点B的坐标为__________;
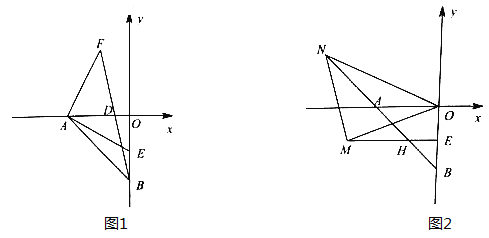
(2)如图1,点E为线段OB上一点,连接AE,过A作AF⊥AE,且AF=AE,连接BF交![]() 轴于点D,若点D(-1,0),求点E的坐标;
轴于点D,若点D(-1,0),求点E的坐标;
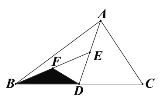
(3)在(2)的条件下,如图2,过E作EH⊥OB交AB于H,点M是射线EH上一点(点M不在线段EH上),连接MO,作∠MON=45°,ON交线段BA的延长线于点N,连接MN,探究线段MN与OM的关系,并说明理由。
【答案】(1)(-4,0) (0,-4)
(2)E(0,-2)
(3)MN⊥OM,MN=OM
【解析】
(1)先将式子变形为完全平方公式的形式,再根据平方的非负性求解;
(2)如图1中,作FH⊥OA于H,由△AFH≌△EAO,推出FH=OA,由△FDH≌△BDO,推出AH=OH=OE=2;
(3)连接OH,OM与BN交于G,由△NGO∽△MGH,推出![]() =
=![]() ,再推出
,再推出![]() =
=![]() ,再得出△NGM∽△OGH,推出∠NMG=∠OHG=90°,推出△OMN是等腰直角三角形即可解决问题.
,再得出△NGM∽△OGH,推出∠NMG=∠OHG=90°,推出△OMN是等腰直角三角形即可解决问题.
(1)∵![]() =0,
=0,
∴a=-4,b=-4,
∴点A的坐标为(-4,0),点B的坐标为(0,-4)
(2)作FH⊥OA于H,
∵AF⊥AE,
∴∠FAE=∠AHF=∠AOE=90°,
∴∠FAH+∠OAE=90°,∠FAH+∠AFH=90°,
∴∠AFH=∠OAE,
∵AF=OA,
∴△AFH≌△EAO,
∴FH=OA,
∵点A(-4,0),点B(0,-4)
∴FH=OA=OB=4,
∵∠FHD=∠BOD=90°,∠FDH=∠BDO,
∴△FDH≌△BDO,
∴OD=DH=1,
∴AH=OH=OE=2,
∴E(0,-2)
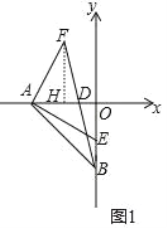
(3)结论:MN=OM,MN⊥OM,
理由:连接OH,OM与BN交于G,
∵OA=OB,∠AOB=45°,
∴∠OAB=45°
∵OE=EB=2,EH∥OA,
∴AH=BH,OH⊥AB,∠AHM=∠OAB=45°,
∵∠MON=45°
∴∠GON=∠GHM,
∵∠NGO=∠MGH,
∴△NGO∽△MGH,
∴![]() =
=![]() ,
,
∴![]() =
=![]() ,
,
∵∠NGM=∠OGH,
∴△NGM∽△OGH,
∴∠NMG=∠OHG=90°,
∴△OMN是等腰直角三角形
∴MN=OM,MN⊥OM.