Question

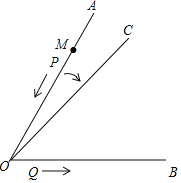
【题目】问题情境：如图1，AB∥CD，∠PAB=130°，∠PCD=120°，求∠APC的度数．

小明的思路是：过P作PE∥AB，通过平行线性质来求∠APC．

(1)按小明的思路，易求得∠APC的度数为_____度；

(2)问题迁移：如图2，AB∥CD，点P在射线OM上运动，记∠PAB=α，∠PCD=β，当点P在B、D两点之间运动时，问∠APC与α、β之间有何数量关系？请说明理由；

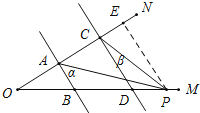
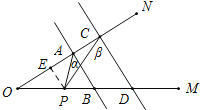
(3)在(2)的条件下，如果点P在B、D两点外侧运动时（点P与点O、B、D三点不重合），请直接写出∠APC与α、β之间的数量关系．

Answer 1

【答案】（1）110°．（2）∠APC=∠α+∠β，（3）当P在BD延长线上时，∠CPA=∠α﹣∠β；当P在DB延长线上时，∠CPA=∠β﹣∠α．

【解析】

试题（1）过点P作PE∥AB，则有PE∥AB∥CD，根据两直线平行，同旁内角互补得到∠A+∠APE=180°，∠C+∠CPE=180°，再根据∠APC=∠APE+∠CPE和已知∠APE和∠CPE度数即可求出∠APC的角度。（2）过P作PE∥AB交AC于E，则有AB∥PE∥CD，进而得到∠α=∠APE，∠β=∠CPE，再根据∠APC=∠APE+∠CPE，即可用α、β来表示∠APC的度数；（3）根据题意画出图形，当P在BD延长线上时，P作PE∥AB交AC于E，则有AB∥PE∥CD，可得到∠CPA=∠β﹣∠α，当如图所示，当P在DB延长线上时，P作PE∥AB交AC于E，则有AB∥PE∥CD，可得到∠CPA=∠β﹣∠α；

试题解析：

（1）解：过点P作PE∥AB，

∵AB∥CD，

∴PE∥AB∥CD，

∴∠A+∠APE=180°，∠C+∠CPE=180°，

∵∠PAB=130°，∠PCD=120°，

∴∠APE=50°，∠CPE=60°，

∴∠APC=∠APE+∠CPE=110°．

（2）∠APC=∠α+∠β，

理由：如图2，过P作PE∥AB交AC于E，

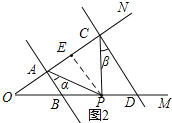
∵AB∥CD，

∴AB∥PE∥CD，

∴∠α=∠APE，∠β=∠CPE，

∴∠APC=∠APE+∠CPE=∠α+∠β；

（3）如图所示，当P在BD延长线上时，

∠CPA=∠α﹣∠β；

如图所示，当P在DB延长线上时，

∠CPA=∠β﹣∠α．