题目内容
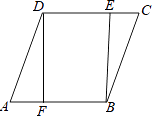
【题目】如图,在Rt△ABC中,∠ACB=90°,以BC为直径的⊙O交AB于点D,E是AC的中点,OE交CD于点F.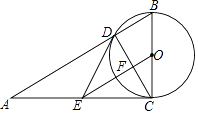
(1)若∠BCD=36°,BC=10,求BD的长;
(2)判断直线DE与⊙O的位置关系,并说明理由;
(3)求证:2CE2=ABEF.
【答案】
(1)解:∵BC是直径,
∴∠BDC=90°,
在Rt△BCD中,∵BC=10,∠BCD=36°,
∴BD=BCsin36°=10sin36°≈5.9.
(2)解:连接OD.
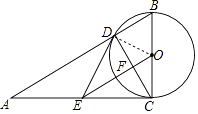
∵AE=EC,OB=OC,
∴OE∥AB,
∵CD⊥AB,
∴OE⊥CD,
∵OD=OC,
∴∠DOE=∠COE,
在△EOD和△EOC中,
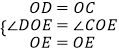 ,
,
∴△EOD≌△EOC,
∴∠EDO=∠ECO=90°,
∴OD⊥DE,
∴DE是⊙O的切线.
(3)解:∵OE⊥CD,
∴DF=CF,∵AE=EC,
∴AD=2EF,
∵∠CAD=∠CAB,∠ADC=∠ACB=90°,
∴△ACD∽△ABC,
∴AC2=ADAB,
∵AC=2CE,
∴4CE2=2EFAB,
∴2CE2=EFAB.
【解析】(1)在直角三角形中,由斜边求对边,用正弦;(2)要证DE是切线,连结OE,证∠EDO是直角,可证△EOD≌△EOC,得出∠EDO=∠ECO=90°;(3)要证2CE2=ABEF,可从![]() 入手,CE2=
入手,CE2=![]() ,所以2CE2=2
,所以2CE2=2![]()
【考点精析】解答此题的关键在于理解直线与圆的三种位置关系的相关知识,掌握直线与圆有三种位置关系:无公共点为相离;有两个公共点为相交,这条直线叫做圆的割线;圆与直线有唯一公共点为相切,这条直线叫做圆的切线,这个唯一的公共点叫做切点,以及对相似三角形的判定与性质的理解,了解相似三角形的一切对应线段(对应高、对应中线、对应角平分线、外接圆半径、内切圆半径等)的比等于相似比;相似三角形周长的比等于相似比;相似三角形面积的比等于相似比的平方.