题目内容
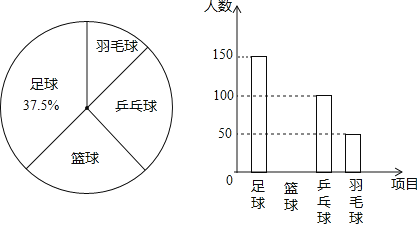
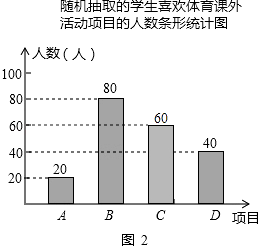
【题目】某学校为了增强学生体质，决定开设以下体育课外活动项目：A篮球、B乒乓球、C跳绳、D踢毽子，为了解学生最喜欢哪一种活动项目，随机抽取了部分学生进行调查，并将调查结果绘制成了两幅不完整的统计图，请回答下列问题：
（1）这次被调查的学生共有人；
（2）请你将条形统计图补充完成；
（3）在平时的乒乓球项目训练中，甲、乙、丙、丁四人表现优秀，现决定从这四名同学中任选两名参加乒乓球比赛，求恰好选中甲、乙两位同学的概率（用树状图或列表法解答）．
【答案】
（1）200
（2）解：补充如图：
（3）列表如下：
甲 | 乙 | 丙 | 丁 | |
甲 | ﹨ | （乙，甲） | （丙，甲） | （丁，甲） |
乙 | （甲，乙） | ﹨ | （丙，乙） | （丁，乙） |
丙 | （甲，丙） | （乙，丙） | ﹨ | （丁，丙） |
丁 | （甲，丁） | （乙，丁） | （丙，丁） | ﹨ |
∵共有12种等可能的情况，恰好选中甲、乙两位同学的有2种，
∴P（选中甲、乙）= 
= 
.
【解析】解：（1）根据题意得：这次被调查的学生共有20÷ 
=200（人）．
故答案为：200；（2）C项目对应人数为：200﹣20﹣80﹣40=60（人）；
（1）根据题意可知这次被调查的学生共有20÷ =200（人）；（2）首先求得C项目对应人数为：200﹣20﹣80﹣40=60（人），进而补全条形统计图即可；（3）首先根据题意列表，求得所有等可能的结果与恰好选中甲、乙两位同学的情况，再利用概率公式即可求得答案.
练习册系列答案
相关题目
