题目内容
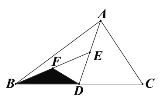
【题目】如图,D、E、F分别为BC、AD、BE的中点,若△BFD的面积为6,则 △ABC的面积等于_____________.
【答案】48
【解析】
由于F是BE的中点,BF=EF,那么△EFD和△BFD可看作等底同高的两个三角形,根据三角形的面积公式,得出△EFD和△BFD的面积相等,进而得出△BDE的面积等于△BFD的面积的2倍;同理,由于E是AD的中点,得出△ADB的面积等于△BDE面积的2倍;由于AD是BC边上的中线,得出△ABC的面积等于△ABD面积的2倍,代入求解即可.
∵F是BE的中点,∴BF=EF,
∴S△EFD=S△BFD,
又∵S△BDE=S△EFD+S△BFD,
∴S△BDE=2S△BFD=2×6=12.
同理,S△ABC=2S△ABD=2×2S△BDE=4×12=48.
故答案为48.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目