题目内容
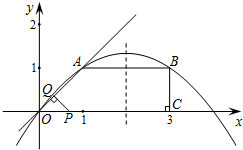
如图,Rt△AOB的两直角边OA、OB的长分别是1和3,将△AOB绕O点按逆时针方向旋转90°,至△DOC的位置.
(1)求过C、B、A三点的二次函数的解析式;
(2)若(1)中抛物线的顶点是M,判定△MDC的形状,并说明理由.

(1)求过C、B、A三点的二次函数的解析式;
(2)若(1)中抛物线的顶点是M,判定△MDC的形状,并说明理由.

(1)由题意知,C、B、A三点的坐标分别为:C(-3,0)、B(0,3)、A(1,0);
设二次函数的解析式为y=a(x-1)(x+3),依题意,有:
a(0-1)(0+3)=3,解得:a=-1
故过C、B、A三点的二次函数的解析式为y=-x2-2x+3.
(2)△MDC是等腰直角三角形,理由如下:
由(1)知,抛物线的解析式:y=-x2-2x+3=-(x+1)2+4,则M(-1,4);
易知:C(-3,0)、D(0,1),则:
MC2=(-1+3)2+(4-0)2=20,MD2=(-1-0)2+(4-1)2=10,CD2=(-3-0)2+(0-1)2=10
则MC2=MD2+CD2,且MD=CD,
因此△MDC为等腰直角三角形.
设二次函数的解析式为y=a(x-1)(x+3),依题意,有:
a(0-1)(0+3)=3,解得:a=-1
故过C、B、A三点的二次函数的解析式为y=-x2-2x+3.
(2)△MDC是等腰直角三角形,理由如下:
由(1)知,抛物线的解析式:y=-x2-2x+3=-(x+1)2+4,则M(-1,4);
易知:C(-3,0)、D(0,1),则:
MC2=(-1+3)2+(4-0)2=20,MD2=(-1-0)2+(4-1)2=10,CD2=(-3-0)2+(0-1)2=10
则MC2=MD2+CD2,且MD=CD,
因此△MDC为等腰直角三角形.

练习册系列答案
相关题目