Question

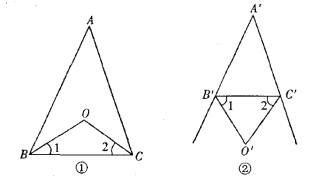
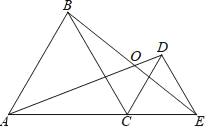
【题目】如图，△ABC和△CDE都是等边三角形，A、C、E在一条直线上．

（1）线段AD与BE相等吗？请证明你的结论；

（2）设AD与BE交于点O，求∠AOE的度数．

Answer 1

【答案】（1）AD＝BE；（2）120°．

【解析】

(1) 利用等边三角形的性质得到一对角相等，一对边相等，利用等式的性质得到夹角相等，利用SAS得到三角形ACD与三角形BCE全等，利用全等三角形的对应边相等即可得证．

(2)利用三角形全等，转化相关角度即可解答.

解：（1）AD＝BE，

理由如下：在等边△ABC和等边△CDE中，

∵∠ACB＝∠DCE＝60°，

∴∠ACD＝∠BCE，

又∵AC＝BC，CD＝CE，

∴△ACD≌△BCE（SAS），

∴AD＝BE．

（2）∵△ACD≌△BCE，

∴∠CAD＝∠CBE，

∵∠ACB＝∠CBE＋∠AEB＝60°，

∴∠CAD＋∠AEB＝60°，

∴∠AOE＝180°﹣（∠CAD＋∠AEB）＝120°．