题目内容
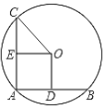
【题目】如图,在⊙O中,AB、AC为互相垂直且相等的两条弦,则下列说法中正确的有( )
①点C、O、B一定在一条直线上;②若点E、点D分别是CA、AB的中点,则OE=OD;③若点E是CA的中点,连接CO,则△CEO是等腰直角三角形.
A. 3个 B. 2个 C. 1个 D. 0个
【答案】A
【解析】
①根据90°的圆周角所对的弦是直径可以作出判断;
②同圆或等圆中相等的弦所对的弦心距相等即可作出判断;
③首先判定四边形OEAD是正方形,然后得到OE=EC即可.
①∵∠A=90°,
∴∠A所对的弦是直径,
∴点C、O、B一定在一条直线上,故正确;
②根据相等的弦所对的弦心距也相等可知当点E、点D分别是CA、AB的中点时,则OE=OD正确;
③∵OD⊥AB于D,OE⊥AC于E,
∴AD=![]() AB,AE=
AB,AE=![]() AC,∠ADO=∠AEO=90°,
AC,∠ADO=∠AEO=90°,
∵AB⊥AC,
∴∠DAE=90°,
∴四边形ADOE是矩形,
∵AB=AC,
∴AD=AE,
∴四边形ADOE是正方形,
∴OE=AE=CE,
∴△CEO是等腰直角三角形,故正确.
故选:A.

练习册系列答案
相关题目