题目内容
【题目】如图，CD是△ABC的角平分线，△ABC的面积为12，BC长为6，点E，F分别是CD，AC上的动点，则AE+EF的最小值是（ ）
A.6B.4C.3D.2
【答案】B
【解析】
根据轴对称的性质得出AE+EF=HE+EF,再根据点到直线的距离垂线段最短得出当HF⊥AC时，HE+EF最小为HF，再根据三角形面积公式计算出AG，根据AH=AG即可得出结论.
解：作A关于CD的对称点H，
∵CD是△ABC的角平分线，
∴点H一定在BC上，且AE+EF=HE+EF
过H作HF⊥AC于F，交CD于E，
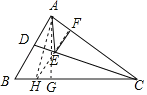
则此时，AE+EF的值最小，AE+EF的最小值＝HF，
过A作AG⊥BC于G，
∵△ABC的面积为12，BC长为6，
∴AG＝4，
∵CD垂直平分AH，
∴AC＝CH，
∴S△ACH＝
ACHF＝CHAG，
∴HF＝AG＝4，
∴AE+EF的最小值是4，
故选：B．
练习册系列答案
相关题目
