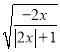题目内容
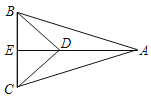
【题目】如图,AE是△ABC的角平分线,D是AE上一点,∠DBE=∠DCE.求证:BE=CE.
【答案】证明见解析
【解析】
作DG⊥AB于G,DH⊥AC于H,证明Rt△BDG≌Rt△CDH且根据全等三角形对应角相等得出∠DBG=∠DCH,由此可得∠ABE=∠ACE,根据等角对等边得出AB=AC,根据等腰三角形三线合一即可得出结论.
证明:作DG⊥AB于G,DH⊥AC于H,如图所示:
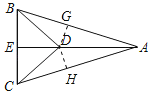
∵AE是△ABC的角平分线,DG⊥AB,DH⊥AC,
∴DG=DH,
∵∠DBE=∠DCE,
∴DB=DC,
在Rt△BDG和Rt△CDH中,
![]() ,
,
∴Rt△BDG≌Rt△CDH(HL),
∴∠DBG=∠DCH,
∵∠DBE=∠DCE,
∴∠ABE=∠ACE,
∴AB=AC,
∵AE是△ABC的角平分线,
∴BE=CE.

练习册系列答案
 春雨教育同步作文系列答案
春雨教育同步作文系列答案
相关题目