题目内容
【题目】在ABCD中,AB=BC=9,∠BCD=120°.点M从点A出发沿射线AB方向移动.同时点N从点B出发,以相同的速度沿射线BC方向移动,连接AN,CM,直线AN、CM相交于点P.
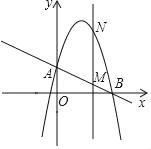
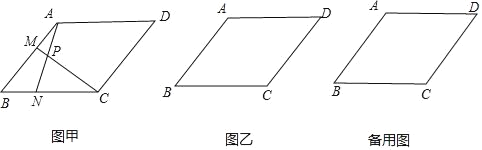
(1)如图甲,当点M、N分别在边AB、BC上时,
①求证:AN=CM;
②连接MN,当△BMN是直角三角形时,求AM的值.
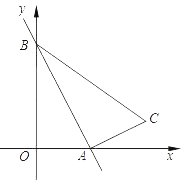
(2)当M、N分别在边AB、BC的延长线上时,在图乙中画出点P,并直接写出∠CPN的度数.
【答案】(1)①见解析②3或6(2)120°
【解析】
(1)①连接AC,先证△ABC是等边三角形得AB=CA=9、∠B=∠CAB=60°,由BN=AM证△ABN≌△CAM即可得;
②分∠MNB=90°和∠NMB=90°两种情况,由∠B=60°得出另一个锐角为30°,根据直角三角形中30°角所对边等于斜边的一半及AM=BN求解可得;
(2)根据题意作出图形,连接AC,先证△BAN≌△ACM得∠N=∠M,由∠NCP=∠MCB知∠CPN=∠CBM,根据AB∥CD、∠BCD=120°可得∠CPN=∠CBM=120°.
(1)①如图1,连接AC,
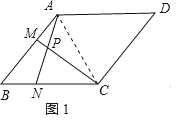
在ABCD中,AB∥DC,
∴∠B=180°﹣∠BCD=180°﹣120°=60°,
又∵AB=BC=9,
∴△ABC是等边三角形,
∴AB=CA=9,∠B=∠CAB=60°,
又∵BN=AM,
∴△ABN≌△CAM(SAS),
∴AN=CM;
②如图2,
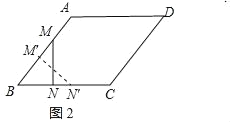
(Ⅰ)当∠MNB=90°时,
∵∠B=60°,
∴∠BMN=90°﹣60°=30°,
∴BN=![]() BM,
BM,
又∵BN=AM,
∴AM=![]() (9﹣AM),
(9﹣AM),
∴AM=3;
(Ⅱ)当∠NMB=90°时,∠BNM=90°﹣60°=30°,
∴BM=![]() BN,
BN,
∴9﹣AM=![]() AM,
AM,
∴AM=6;
综上所述,当△BMN是直角三角形时,AM的值为3或6;
(2)如图3所示,
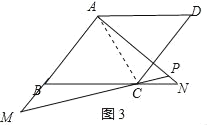
点P即为所求;
∠CPN=120°,
连接AC,
由(1)知△ABC是等边三角形,
∴∠BAN=∠CAM=60°、AB=CA,
又∵BN=AM,
∴△BAN≌△ACM(SAS),
∴∠N=∠M,
∵∠NCP=∠MCB,
∴∠CPN=∠CBM,
∵AB∥CD,∠BCD=120°,
∴∠CPN=∠CBM=120°.