题目内容
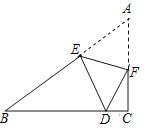
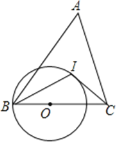
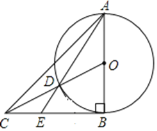
【题目】如图,AB=BC=2,∠ABC=90°,以AB为直径的⊙O交OC于点D,AD的延长线交BC于点E,则BE的长为______.
【答案】![]() -1
-1
【解析】
先根据已知和勾股定理得出CD的长,再根据直径所对的圆周角为直角和等腰三角形的性质证得∠CDE=∠CBD,然后根据两角对应相等两三角形相似得出△CDE∽△CBD,可得比例式,从而得到CD2=CECB,求得CE即可解决问题.
解:连接BD.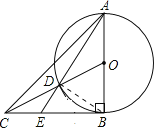
∵∠CBO=90°,BC=2,OB=1,
∴OC=![]() ,
,
∴CD=OC-OD=![]() -1,
-1,
∵AB是直径,
∴∠ADB=∠EDB=90°,
∴∠CDE+∠ODB=90°,
∵OD=OB,
∴∠ODB=∠OBD,
∵∠CBD+∠OBD=90°,
∴∠CDE=∠CBD,
∵∠DCE=∠BCD,
∴△CDE∽△CBD,
∴CD2=CECB,
∴CE=3-![]() ,
,
∴BE=BC-CE=![]() -1.
-1.
故答案为![]() -1.
-1.

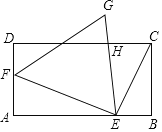
【题目】问题提出:求n个相同的长方体(相邻面的面积不相同)摆放成一个大长方体的表面积.
问题探究:探究一:
为了研究这个问题,同学们建立了如下的空间直角坐标系:空间任意选定一点O,以点O为端点,作三条互相垂直的射线ox、oy、oz.这三条互相垂直的射线分别称作x轴、y轴、z轴,统称为坐标轴,它们的方向分别为ox(水平向前)、oy(水平向右)、oz(竖直向上)方向.
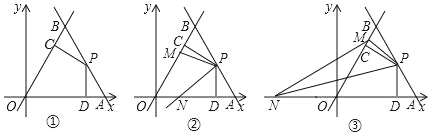
将相邻三个面的面积记为S1、S2、S3,且S1<S2<S3的小长方体称为单位长方体,现将若干个单位长方体在空间直角坐标系内进行码放,要求码放时将单位长方体S1所在的面与x轴垂直,S2所在的面与y轴垂直,S3所在的面与z轴垂直,如图1所示.
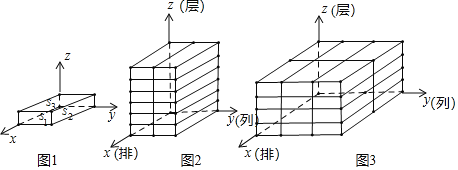
若将x轴方向表示的量称为几何体码放的排数,y轴方向表示的量称为几何体码放的列数,z轴方向表示的量称为几何体码放的层数;如图2是由若干个单位长方体在空间直角坐标系内码放的一个几何体,其中这个几何体共码放了1排2列6层,用有序数组记作(1,2,6),如图3的几何体码放了2排3列4层,用有序数组记作(2,3,4).这样我们就可用每一个有序数组(x,y,z)表示一种几何体的码放方式.
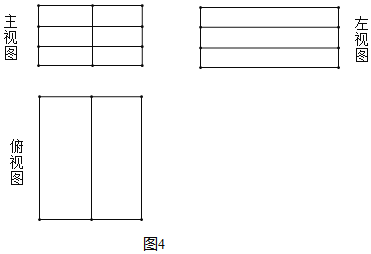
问题一:如图4是由若干个单位长方体码放的一个几何体的三视图,则这种码放方式的有序数组为______.
组成这个几何体的单位长方体的个数为______个.
探究二:
为了探究有序数组(x,y,z)的几何体的表面积公式S(x,y,z),同学们针对若干个单位长方体进行码
放,制作了下列表格
几何体 有序数组 | 单位长方体的个数 | 表面上面积为S1的个数 | 表面上面积为S2的个数 | 表面上面积为S3的个数 | 表面积 |
(1,1,1) | 1 | 2 | 2 | 2 | 2S1+2S2+2S3 |
(1,2,1) | 2 | 4 | 2 | 4 | 4S1+2S2+4S3 |
(3,1,1) | 3 | 2 | 6 | 6 | 2S1+6S2+6S3 |
(2,1,2) | 4 | 4 | 8 | 4 | 4S1+8S2+4S3 |
(1,5,1) | 5 | 10 | 2 | 10 | 10S1+2S2+10S3 |
(1,2,3) | 6 | ||||
…… | …… | …… | …… | …… | …… |
问题二:请将上面表格补充完整:当单位长方体的个数是6时,表面上面积为S1的个数是______.
表面上面积为S2的个数是______;表面上面积为S3的个数是______;表面积为______.
问题三:根据以上规律,请写出有序数组(x,y,z)的几何体表面积计算公式S(x,y,z)=______(用x、y、z、S1、S2、S3表示)
探究三:
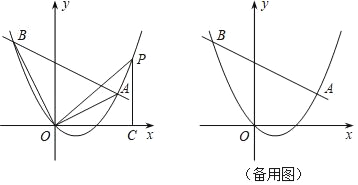
同学们研究了当S1=2,S2=3,S3=4时,用3个单位长方体码放的几何体中,有三种码放的方法,有序数组分别为(1,1,3),(1,3,1),(3,1,1).而S(1,1,3)=38,S(1,3,1)=42,S(3,1,1)=46.容易发现个数相同的长方体,由于码放的方法不同,组成的几何体的表面积就不同.
拓展应用:
要将由20个相同的长方体码放的几何体进行打包,其中每个长方体的长是8,宽是5,高是6.为了节约外包装材料,请直接写出使几何体表面积最小的有序数组,并写出这个最小面积(不需要写解答过程).(缝隙不计)
【题目】垫球是排球队常规训练的重要项目之一.下列图表中的数据是甲、乙、丙三人每人十次垫球测试的成绩.测试规则为连续接球10个,每垫球到位1个记1分.运动员甲测试成绩表
测试序号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
成绩(分) | 7 | 6 | 8 | 7 | 7 | 5 | 8 | 7 | 8 | 7 |
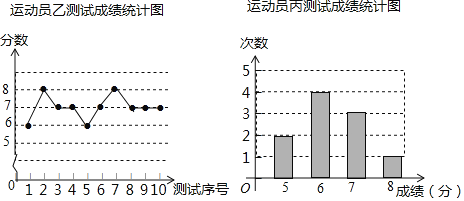
(1)写出运动员甲测试成绩的众数和中位数;
(2)在他们三人中选择一位垫球成绩优秀且较为稳定的接球能手作为自由人,你认为选谁更合适?为什么?(参考数据:三人成绩的方差分别为S甲2=0.8、S乙2=0.4、S丙2=0.8)