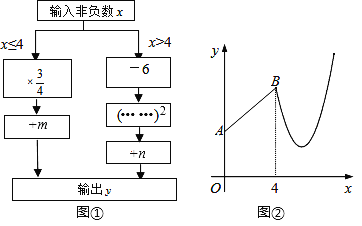
题目内容
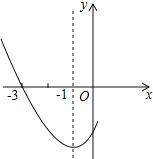
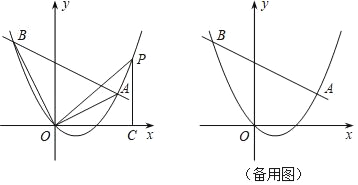
【题目】如图,在平面直角坐标系中,直线y=kx﹣4k+4与抛物线y=![]() x2﹣x交于A、B两点.
x2﹣x交于A、B两点.
(1)直线总经过定点,请直接写出该定点的坐标;
(2)点P在抛物线上,当k=﹣![]() 时,解决下列问题:
时,解决下列问题:
①在直线AB下方的抛物线上求点P,使得△PAB的面积等于20;
②连接OA,OB,OP,作PC⊥x轴于点C,若△POC和△ABO相似,请直接写出点P的坐标.
【答案】(1)![]() ;(2)①P点坐标为
;(2)①P点坐标为![]() ,
,![]() ;②
;② ![]() ,
,![]() ,
,![]() ,
,![]() .
.
【解析】
(1)直线方程化为y=k(x-4)+4,对于任意k点总有一个坐标能满足;(2)作PQ∥y轴,求出PQ,再由S△PAB等于20,根据三角形面积计算公式即可求出相应的坐标;AO=![]() ,BO=
,BO=![]() ,AB=
,AB=![]() ,再根据勾股定理和相似三角形的定义即可求出
,再根据勾股定理和相似三角形的定义即可求出![]() ,进而可求得P3和P4的值.
,进而可求得P3和P4的值.
⑴ ![]() ;
;
直线方程化为![]() ,显然,对于任意的k,点
,显然,对于任意的k,点![]() 的坐标总能满足直线方程.
的坐标总能满足直线方程.
⑵ 当![]() 时,直线方程为
时,直线方程为![]() .
.
联立方程组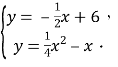 解得
解得![]() ,
,![]() .
.
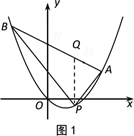
① 如图1,作![]() ∥
∥![]() 轴,交AB于点Q,则
轴,交AB于点Q,则
![]() .
.
![]()
![]() 。
。
令![]() ,即
,即![]() ,解得当
,解得当![]() 或4,相应的P点坐标为
或4,相应的P点坐标为![]() ,
,![]() ;
;
② ![]() ,
,![]() ,
,![]() ,
,![]() .
.
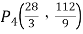
![]() ,
,![]() ,
,![]() .
.
∵![]() ,∴
,∴![]() .
.
(i)△POC∽△ABO时,![]() .
.
即![]() .解得
.解得![]() ,
,![]() ,
,
得![]() ,
,![]() ;
;
(ii)△POC∽△BAO时,![]() .
.
即![]() .解得
.解得![]() ,
,![]() .
.
得![]() ,
,![]() .
.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
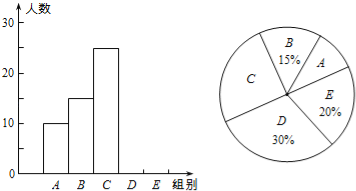
【题目】某校举行“汉字听写”比赛,每位学生听写汉字39个,比赛结束后随机抽查部分学生的听写结果,以下是根据抽查结果绘制的统计图的一部分.
组别 | 正确字数x | 人数 |
A | 0≤x<8 | 10 |
B | 8≤x<16 | 15 |
C | 16≤x<24 | 25 |
D | 24≤x<32 | m |
E | 32≤x<40 | n |
根据以上信息解决下列问题:
(1)在统计表中,m= ,n= ,并补全条形统计图.
(2)扇形统计图中“C组”所对应的圆心角的度数是 .
(3)若该校共有900名学生,如果听写正确的个数少于24个定为不合格,请你估计这所学校本次比赛听写不合格的学生人数.