��Ŀ����
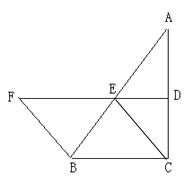
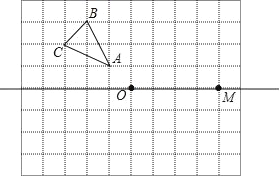
����Ŀ����ͼ����֪����ABCD�У�BC=2cm��AB=2![]() cm����E�ڱ�AB�ϣ���F�ڱ�AD�ϣ���E��A��B�˶�������EC��EF�����˶��Ĺ����У�ʼ�ձ���EC��EF����EFGΪ�ȱ������Σ�
cm����E�ڱ�AB�ϣ���F�ڱ�AD�ϣ���E��A��B�˶�������EC��EF�����˶��Ĺ����У�ʼ�ձ���EC��EF����EFGΪ�ȱ������Σ�
��1����֤��AEF�ס�BCE��
��2����BE�ij�Ϊxcm��AF�ij�Ϊycm����y��x�ĺ�����ϵʽ����д���߶�AF���ķ�Χ��
��3������H��EG���е㣬��˵��A��E��H��F�ĵ���ͬһ��Բ�ϣ������ڵ�E��A��B�˶������У���H�ƶ��ľ��룮
���𰸡���1�������������2��![]() ,
,![]() ��(3)3.
��(3)3.
��������
��1���ɡ�A=��B=90������AFE=��BEC���á�AEF�ס�BCE����2���ɣ�1����AEF��BCE��![]() ��
��![]() ����
����![]() ��Ȼ��������ֵ����3������FH��ȡEF���е�M��֤MA=ME=MF=MH����A��E��H��F��ͬһԲ�ϣ�����AH��֤��EFH=30����A��E��H��F��ͬһԲ�ϣ��á�EAH=��EFH=30�����߶�AH��ΪH�ƶ���·������ֱ��������ABH�У�
��Ȼ��������ֵ����3������FH��ȡEF���е�M��֤MA=ME=MF=MH����A��E��H��F��ͬһԲ�ϣ�����AH��֤��EFH=30����A��E��H��F��ͬһԲ�ϣ��á�EAH=��EFH=30�����߶�AH��ΪH�ƶ���·������ֱ��������ABH�У�![]() ���ɽ�һ����AH.
���ɽ�һ����AH.
�⣺��1���ھ���ABCD�У���A=��B=90����
���AEF+��AFE=90����
��EF��CE��
���AEF+��BEC=90����
���AFE=��BEC��
���AEF�ס�BCE��
��2���ɣ�1����AEF��BEC��
![]() ��
��![]() ��
��
��![]() ��
��
��![]() =
=![]() ��
��
��![]() ʱ��y�����ֵΪ
ʱ��y�����ֵΪ![]() ��
��
��![]() ��
��
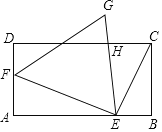
��3����ͼ1������FH��ȡEF���е�M��
�ڵȱ�������EFG�У��ߵ�H��EG���е㣬
���EHF=90����
��ME=MF=MH��
��ֱ��������AEF�У�MA=ME=MF��
��MA=ME=MF=MH��
��A��E��H��F��ͬһԲ�ϣ�
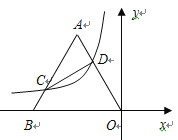
��ͼ2������AH��
�ߡ�EFGΪ�ȱ������Σ�HΪEG�е㣬���EFH=30��
��A��E��H��F��ͬһԲ�ϡ��EAH=��EFH=30����
��ͼ2��ʾ���߶�AH��ΪH�ƶ���·����
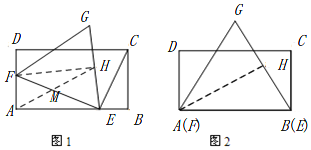
��ֱ��������ABH�У�![]() ��
��
��AB=![]() ��
��
��AH=3��
���Ե�H�ƶ��ľ���Ϊ3��

 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�