题目内容
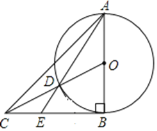
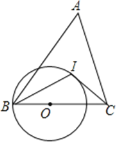
【题目】如图,△ABC中,AC=BC,点I是△ABC的内心,点O在边BC上,以点O为圆心,OB长为半径的圆恰好经过点I,连接CI,BI.
(1)求证:CI是⊙O的切线;
(2)若AC=BC=5,AB=6,求BI的长.
【答案】(1)见解析;(2)![]() .
.
【解析】
(1)设∠ICB=x,∠IBC=y,得:2x+2y+2y=180°,则x+2y=90°,再证明∠IOC+∠ICO=2y+x=90°,可得∠OIC=90°,则CI是⊙O的切线;
(2)延长CI交AB于D,先计算∠CDA=90°,得CD=4,证明△OIC∽△BDC,列比例式![]() ,设⊙O的半径为r,得r的值,由
,设⊙O的半径为r,得r的值,由![]() ,计算DI的值,根据勾股定理可得结论.
,计算DI的值,根据勾股定理可得结论.
(1)证明:连接OI,
∵点I是△ABC的内心,
∴BI、CI分别是∠ABC、∠ACB的平分线,
设∠ICB=x,∠IBC=y,
∵AC=BC,
∴∠ABC=∠A=2y,∠ACB=2x,
∴2x+2y+2y=180°,
∴x+2y=90°,
∵OB=OI,
∴∠OIB=∠OBI,
∴∠ABI=∠OIB,
∴OI∥AB,
∴∠IOC=∠ABC=2y,
∴∠IOC+∠ICO=2y+x=90°,
∴∠OIC=90°,
∴CI是⊙O的切线;
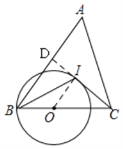
(2)解:延长CI交AB于D,
∵∠ACD+∠A=x+2y=90°,
∴∠CDA=90°,
∴CD⊥AB,
∵AC=BC=5,AB=6,
∴AD=BD=3,
∴CD=4,
∵OI∥AB,
∴△OIC∽△BDC,
∴![]() ,
,
设⊙O的半径为r,
∴![]() ,∴r=
,∴r=![]() ,
,
∵OI∥BD,∴![]() ,
,
∴![]() ,∴DI=
,∴DI=![]() ,
,
由勾股定理得:BI=![]() =
=![]() .
.

练习册系列答案
 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案
相关题目