题目内容
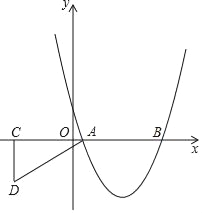
【题目】如图①,直线y=﹣![]() x+8
x+8![]() 与x轴交于点A,与直线y=
与x轴交于点A,与直线y=![]() x交于点B,点P为AB边的中点,作PC⊥OB与点C,PD⊥OA于点D.
x交于点B,点P为AB边的中点,作PC⊥OB与点C,PD⊥OA于点D.
(1)填空:点A坐标为 ,点B的坐标为 ,∠CPD度数为 ;
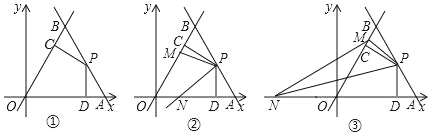
(2)如图②,若点M为线段OB上的一动点,将直线PM绕点P按逆时针方向旋转,旋转角与∠AOB相等,旋转后的直线与x轴交于点N,试求MBAN的值;
(3)在(2)的条件下,当MB<2时(如图③),试证明:MN=DN﹣MC;
(4)在(3)的条件下,设MB=t,MN=s,直接写出s与t的函数表达式.
【答案】(1)(8,0),(4,4![]() ),120°.(2)16;(3)证明见解析;(4)S=
),120°.(2)16;(3)证明见解析;(4)S=![]() +t﹣4(0<t<2).
+t﹣4(0<t<2).
【解析】分析:(1)利用待定系数法可得A、B两点坐标,根据tan∠BOA=![]() ,可得∠BOA=60°,再根据四边形内角和定理可求∠CPD;
,可得∠BOA=60°,再根据四边形内角和定理可求∠CPD;
(2)只要证明△PAN∽△MBP,可得![]() ,由此即可解决问题;
,由此即可解决问题;
(3)如图③中,在DO上截取DK=MC,连接OP.只要证明△PCM≌△PDK,△PNM≌△PNK即可解决问题;
(4)利用(2)(3)中的结论即可解决问题;
详解:(1)如图①中,
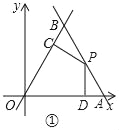
对于直线y=﹣![]() x+8
x+8![]() ,令y=0,解得x=8,可得A(8,0),
,令y=0,解得x=8,可得A(8,0),
由![]() ,解得
,解得![]() ,
,
∴B(4,4![]() ),
),
∴tan∠BOA=![]() ,
,
∴∠BOA=60°,
∵PC⊥OB与点C,PD⊥OA于点D,
∴∠PCO=∠PDO=90°,
∴∠CPD=120°,
故答案为(8,0),(4,4![]() ),120°.
),120°.
(2)如图②中,
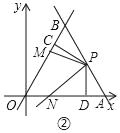
∵OA=OB=8,∠AOB=60°,
∴△AOB是等边三角形,
∴AB=OA=OB=8,∠OBA=∠OAB=60°,
∴PA=PB=4,
∵∠APM=∠APN+∠MPN=∠PMB+∠PBM,
∵∠MPN=∠PBM=60°,
∴∠APN=∠PMB,
∴△PAN∽△MBP,
∴![]() ,
,
∴MBAN=4×4=16.
(3)如图③中,在DO上截取DK=MC,连接OP.
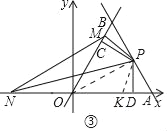
∵OB=OA,PB=PA,
∴∠POB=∠POA,
∵PC⊥OB与点C,PD⊥OA于点D,
∴PC=PD,∵∠PCM=∠PDK=90°,MC=DK,
∴△PCM≌△PDK,
∴PM=PK,∠CPM=∠DPK,
∴∠MPK=∠CPD=120°,
∵∠MPN=60°,
∴∠MPN=∠KPN=60°,∵PN=PN,
∴△PNM≌△PNK,
∴MN=KN=DN﹣DK=DN﹣CM.
(4)如图③中,由(2)可知:AN=![]() ,易知BC=AD=2,
,易知BC=AD=2,
∵MN=DN﹣CM,
∴MN=(AN﹣AD)﹣(BC﹣BM),
∴S=![]() ﹣2﹣(2﹣t)=
﹣2﹣(2﹣t)=![]() +t﹣4(0<t<2).
+t﹣4(0<t<2).

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案