题目内容
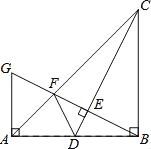
【题目】如图在Rt△ABC中,∠ACB=90°,AC=3,BC=4,点E、F分别在边AB、AC上,将△AEF沿直线EF折叠,使点A的对应点D恰好落在边BC上.若△BDE是直角三角形,则CF的长为______.
【答案】![]() 或
或![]()
【解析】
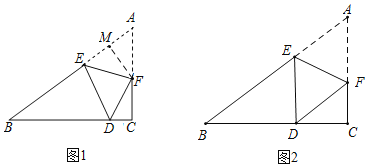
分两种情况:①∠BED=90°,过点F作FM⊥AE,根据折叠性质可知∠AEF=∠DEF=45°,设FC=a,则AF=3-a,在Rt△AMF中用a表示出AE,从而得到BE=5-AE,在Rt△BED中,根据三角函数用a表示BE,则构造出关于a的方程;②∠BDE=90°,证明∠A=∠DFC,根据三角函数找到FC和DF关系即可.
解:①当∠BED=90°时,过点F作FM⊥AE,
根据折叠性质可知∠AEF=∠DEF=45°,
设FC=a,则AF=3-a,在Rt△AMF中,
sinA=![]() ,∴MF=
,∴MF=![]() =ME.
=ME.
cosA=![]() ,∴AM=
,∴AM=![]() .
.
∴AE=AM+MF=![]() =DE.
=DE.
则BE=AB-AE=5-![]() .
.
在Rt△BED中,tanB=![]() ,∴BE=
,∴BE=![]() .
.
∴5-![]() =
=![]() ,解得a=
,解得a=![]() ;
;
②当∠EDB=90°时,
根据折叠性质可知AF=FD,∠A=∠EDF,
∵ED∥AC,∴∠EDF=∠DFC.
∴∠A=∠DFC.
∴cosA=cos∠DFC=![]() ,设FC=x,则AF=3-x=DF,
,设FC=x,则AF=3-x=DF,
∴![]() ,解得x=
,解得x=![]() .
.
综上所述CF长为![]() 或
或![]() .
.

【题目】为了让同学们了解自己的体育水平,初二1班的体育刘老师对全班45名学生进行了一次体育模拟测试(得分均为整数),成绩满分为10分,1班的体育委员根据这次测试成绩,制作了统计图和分析表如下:
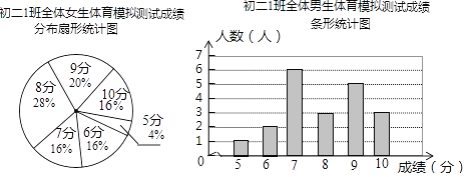
初二1班体育模拟测试成绩分析表
平均分 | 方差 | 中位数 | 众数 | |
男生 | 2 | 8 | 7 | |
女生 | 7.92 | 1.99 | 8 |
根据以上信息,解答下列问题:
(1)这个班共有男生________人,共有女生________人;
(2)补全初二1班体育模拟测试成绩分析表.