题目内容
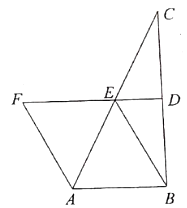
【题目】如图,在平行四边形ABCD中,点E,F在对角线AC上,且AE=CF。
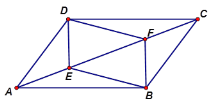
(1)求证:四边形DEBF是平行四边形;
(2)若DE=3,CD=4,∠EDC=90°,当四边形DEBF是菱形时,AE的长为多少?
【答案】(1)详见解析;(2)![]()
【解析】
(1)本题中,连接BD交AC于O,则可知OB=OD,OA=OC,又AE=CF,所以OE=OF,然后依据对角线互相平分的四边形是平行四边形即可证明.
(2)因为DE=3,CD=4,∠EDC=90°,由勾股定理得![]() 5,再根据菱形的对角线互相平分和面积公式计算出
5,再根据菱形的对角线互相平分和面积公式计算出![]() ,再根据勾股定理解得
,再根据勾股定理解得![]() ,即可解答.
,即可解答.
证明:(1)如图,连接BD,与AC相交于点O
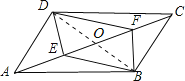
∵四边形ABCD为平行四边形
∴OB=OD.OA=OC
∵AE=CF
∴OE=OF
∴四边形DEBF为平行四边形.
(2)在RtΔCDE中![]()
∵四边形DEBF为菱形
∴BD⊥EF
∴![]() .
.
∴![]()
∴![]()
∴![]() .
.

练习册系列答案
 百强名校期末冲刺100分系列答案
百强名校期末冲刺100分系列答案 好成绩1加1期末冲刺100分系列答案
好成绩1加1期末冲刺100分系列答案 金状元绩优好卷系列答案
金状元绩优好卷系列答案
相关题目