��Ŀ����
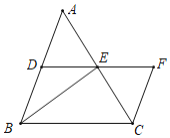
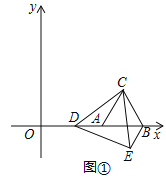
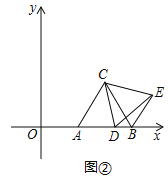
����Ŀ����ͼ�٣���ƽ��ֱ������ϵ�У��ȱߡ�ABC�Ķ���A��B������ֱ�Ϊ��5��0������9��0������D��x����������һ�����㣬����CD������ACD�Ƶ�C��ʱ����ת60���õ���BCE������DE��
������ֱ��д����C�����꣬���жϡ�CDE����״��˵�����ɣ�
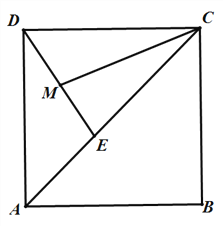
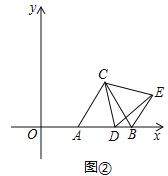
��������ͼ�ڣ�����D���߶�AB���˶�ʱ����BDE���ܳ��Ƿ������Сֵ�������ڣ������BDE����С�ܳ�����ʱ��D�����ꣻ�������ڣ�˵�����ɣ�
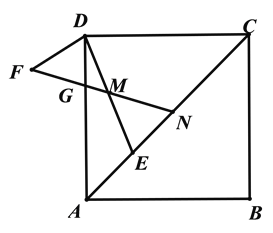
����������BDE��ֱ��������ʱ�����D�����꣮��ֱ��д��������ɣ�
���𰸡�����C![]() ����CDE�ǵȱ���������������������
����CDE�ǵȱ���������������������![]() ��D��7��0��������D��1��0����13��0����
��D��7��0��������D��1��0����13��0����
��������������
��1����ͼ1������C��CH��x���ڵ�H���ɡ�ABC�ǵȱ���������AH=![]() AB=2�����AC=AB=4��OA=5���ɵ�CH=
AB=2�����AC=AB=4��OA=5���ɵ�CH=![]() ��OH=7���ɴ˼��ɵõ���C�����ꣻ����ת�����ʿ�֪CE=CD�������ת�ǡ�DCE=60���֪��CDE�ǵȱ������Σ�
��OH=7���ɴ˼��ɵõ���C�����ꣻ����ת�����ʿ�֪CE=CD�������ת�ǡ�DCE=60���֪��CDE�ǵȱ������Σ�
��2����ͼ2���ɣ�1����֪��CDE�ǵȱ������Σ��ɴ˿ɵ�DE=CD���ɡ�CDE���ɡ�CAD�Ƶ�C��ת�õ��ģ��ɴ˿ɵ�BE=AD���Ӷ��ɵá�BDE���ܳ�=BD+BE+DE=BD+AD+CD=AB+CD=4+CD���ɴ˿�֪����CD��ABʱ��CD��С����ʱ��BDE���ܳ���С���ɣ�1����֪����ʱCD=![]() ��OD=7��������D������Ϊ��7��0��ʱ����BDE���ܳ���С����СֵΪ
��OD=7��������D������Ϊ��7��0��ʱ����BDE���ܳ���С����СֵΪ![]() ��
��
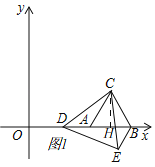
��3����ͼ3������CBE=��CAD=120���ɵ���ABC=60�㣬�ɴ˿ɵ���DBE=60���90�㣬�����BDE��ֱ�������Σ���֪�������١�BED=90�㣻�ڡ�BDE=90������ͼ3����BD'E'=90������������������������������Ҫ���ͼ�Σ��������֪�������з������㼴��.
��⣺
������ͼ1������C��CH��AB��H��
�ߡ�ABC�ǵȱ������Σ�CH��AB�ڵ�H��
���AHC=90����AH=![]() AB=
AB=![]() ��9��5��=2��
��9��5��=2��
��OH=OA+AH=7��
��AC=AB=4��
����Rt��ACH��CH=![]() ��
��
�� C![]() ��
��
�ߡ�CBE������CAD�Ƶ�C��ʱ����ת60��õ��ģ�
���DCE=60�㣬DC=EC��
���CDE�ǵȱ������Σ�
���������ڣ�������������ͼ2���ɣ�����֪����CDE�ǵȱ������Σ�
��DE=CD��
����ת֪��BE=AD��
��C��DBE=BE+DB+DE=AB+DE=4+DE=4+CD��
�ɴ��߶���̿�֪��CD��AB��Dʱ����BDE���ܳ���С����ʱ������1����֪CD=2![]() ��OD=7��
��OD=7��
���BDE���ܳ���СֵΪ4+2![]() ����D��7��0����
����D��7��0����
��������ͼ3��
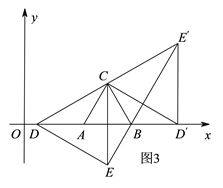
������ת֪����CBE=��CAD=120�㣬
�ߡ�ABC=60�㣬
���DBE=60���90�㣬
�ߡ�BDE��ֱ�������Σ�
��������BED=90������BDE=90������ͼ3����BD'E'=90�㣩���������
������BED=90��ʱ��
�ߡ�CDE�ǵȱ������Σ�
���CED=60�㣬
���BEC=30�㣬
�ߡ�CBE=��CAD=120�㣬
���BCE=30�㣬
��BE=BC=AB=4��
��Rt��BDE�У���DBE=��CBE����ABC=60�㣬
��BD=2BE=8��
��OB=9��
��OD=OB��BD=1��
��D��1��0����
������BD'E'=90��ʱ��
�ߡ�CD'E'�ǵȱ������Σ�
���CD'E'=60�㣬
���BD'C=30�㣬
�ߡ�ABC=60�㣬
���BCD'=30��=��BD'E��
��BD'=BC=6��
��OB=9��
��OD'=OB+BD'=13��
��D'��13��0����
�������ڵ�Dʹ��BDE��ֱ�������Σ���ʱ��D������ֱ�Ϊ����1��0����13��0����

 �Ͻ�ƽСѧ��������ϵ�д�
�Ͻ�ƽСѧ��������ϵ�д�