题目内容
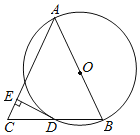
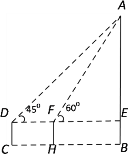
【题目】乐至县城有两座远近闻名的南北古塔,清朝道光11年至13年(公元1831--1833年)修建,南塔名为“文运塔”,高30米;北塔名为“凌云塔”.为了测量北塔的高度AB,身高为1.65米的小明在C处用测角仪CD,(如图所示)测得塔顶A的仰角为45°,此时小明在太阳光线下的影长为1.1米,测角仪的影长为1米.随后,他再向北塔方向前进14米到达H处,又测得北塔的顶端A的仰角为60°,求北塔AB的高度.(参考数据![]() ≈1.414,
≈1.414,![]() ≈1.732,结果保留整数)
≈1.732,结果保留整数)

【答案】北塔的高度AB约为35米.
【解析】
设AE=x,根据在同一时间,物体高度与影子长度成正比例关系可得CD的长,在Rt△ADE中,由∠ADE=45°可得AE=DE=x,可得EF=(x-14)米,在Rt△AFE中,利用∠AFE的正切列方程可求出x的值,根据AB=AE+BE即可得答案.
设AE=x,
∵小明身高为1.65米,在太阳光线下的影长为1.1米,测角仪CD的影长为1米,
∴![]()
∴CD=1.5(米)
∴BE=CD=1.5(米),
∵在Rt△ADE中,∠ADE=45°,
∴DE=AE=x,
∵DF=14米,
∴EF=DE-DF=(x-14)米,
在Rt△AFE中,∠AFE=60°,
∴tan60°=![]() =
=![]() ,
,
解得:x=(![]() )(米),
)(米),
故AB=AE+BE=![]() +1.5≈35米.
+1.5≈35米.
答:北塔的高度AB约为35米.

 名校课堂系列答案
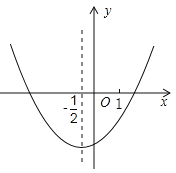
名校课堂系列答案【题目】在函数学习中,我们经历了“确定函数表达式﹣﹣利用函数图象研究其性质﹣﹣运用函数解决问题”的学习过程.在画函数图象时,我们通过描点或平移的方法画出了所学的函数图象.同时我们也学习了绝对值的意义![]() ,结合上面经历的学习过程,现在来解决下面的问题:在函数y=|kx﹣1|+b中,当x=2时,y=﹣3;x=0时,y=﹣2.
,结合上面经历的学习过程,现在来解决下面的问题:在函数y=|kx﹣1|+b中,当x=2时,y=﹣3;x=0时,y=﹣2.
(1)求这个函数的表达式;
(2)用列表描点的方法画出该函数的图象;请你先把下面的表格补充完整,然后在下图所给的坐标系中画出该函数的图象;
x | … | ﹣6 | ﹣4 | ﹣2 | 0 | 2 | 4 | 6 | … |
y | … |
| 0 | ﹣1 | ﹣2 | ﹣3 | ﹣2 |
| … |
(3)观察这个函数图象,并写出该函数的一条性质;
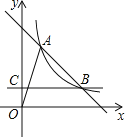
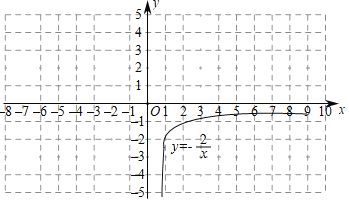
(4)已知函数y=![]() (x>0)的图象如图所示,与y=|kx﹣1|+b的图象两交点的坐标分别是(2
(x>0)的图象如图所示,与y=|kx﹣1|+b的图象两交点的坐标分别是(2![]() +4,
+4,![]() -2),(2
-2),(2![]() ﹣2
﹣2![]() ﹣1),结合你画的函数图象,直接写出|kx﹣1|+b≤
﹣1),结合你画的函数图象,直接写出|kx﹣1|+b≤![]() 的解集.
的解集.