Question

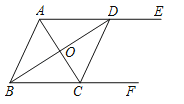
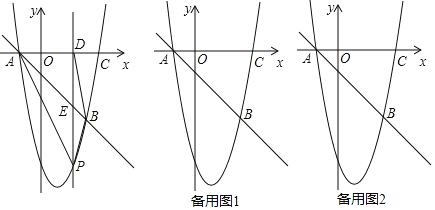
【题目】问题情境:在综合实践课上，老师让同学们以“菱形纸片的剪拼”为主题开展数学活动，如图（1），将一张菱形纸片ABCD（∠BAD＝60°）沿对角线AC剪开，得到△ABC和△ACD

操作发现:（1）将图（1）中的△ABC以A为旋转中心，顺时针方向旋转角α（0°＜α＜60°）得到如图（2）所示△ABC′，分别延长BC′和DC交于点E，发现CE＝C′E．请你证明这个结论．

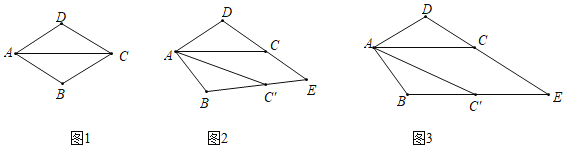
（2）在问题（1）的基础上，当旋转角α等于多少度时，四边形ACEC′是菱形？请你利用图（3）说明理由．

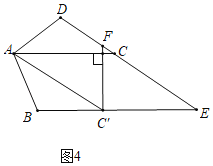
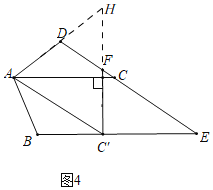
拓展探究:（3）在满足问题（2）的基础上，过点C′作C′F⊥AC，与DC交于点F．试判断AD、DF与AC的数量关系，并说明理由．

Answer 1

【答案】（1）见解析；（2）当α＝30°时，四边形AC′EC是菱形，理由见解析；（3）AD+DF＝AC，理由见解析

【解析】

（1）先判断出∠ACC′=∠AC′C，进而判断出∠ECC′=∠EC′C，即可得出结论；
（2）判断出四边形AC′EC是平行四边形，即可得出结论；
（3）先判断出HAC′是等边三角形，得出AH=AC′，∠H=60°，再判断出△HDF是等边三角形，即可得出结论．

（1）证明：如图2，连接CC′，

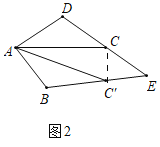
∵四边形ABCD是菱形，

∴∠ACD＝∠AC′B＝30°，AC＝AC′，

∴∠ACC′＝∠AC′C，

∴∠ECC′＝∠EC′C，

∴CE＝C′E；

（2）当α＝30°时，四边形AC′EC是菱形，

理由：∵∠DCA＝∠CAC′＝∠AC′B＝30°，

∴CE∥AC′，AC∥C′E，

∴四边形AC′EC是平行四边形，

又∵CE＝C′E，

∴四边形AC′EC是菱形；

（3）AD+DF＝AC．

理由：如图4，分别延长CF与AD交于点H，

∵∠DAC＝∠C′AC＝30°，C′F⊥AC，

∴∠AC′H＝∠DAC′＝60°，

∴△HAC′是等边三角形，

∴AH＝AC′，∠H＝60°，

又∵AD＝DC，

∴∠DAC＝∠DCA＝30°，

∴∠HDC＝∠DAC+∠DCA＝60°，

∴△HDF是等边三角形，

∴DH＝DF，

∴AD+DF＝AD+DH＝AH．

∵AC′＝AC，

∴AC＝AD+DF．