题目内容
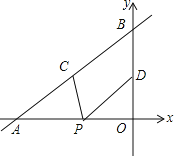
【题目】已知:如图,点P是一个反比例函数的图象与正比例函数y=﹣2x的图象的公共点,PQ垂直于x轴,垂足Q的坐标为(2,0).
(1)求这个反比例函数的解析式;
(2)如果点M在这个反比例函数的图象上,且△MPQ的面积为6,求点M的坐标.

【答案】(1)y=﹣![]() ;(2)M(5,﹣
;(2)M(5,﹣![]() )或(﹣1,8).
)或(﹣1,8).
【解析】
(1)由Q(2,0),推出P(2,-4),利用待定系数法即可解决问题;
(2)根据三角形的面积公式求出MN的长,分两种情形求出点M的坐标即可.
(1)把x=2代入y=﹣2x得 y=﹣4
∴P(2,﹣4),
设反比例函数解析式y=![]() (k≠0),
(k≠0),
∵P在此图象上
∴k=2×(﹣4)=﹣8,
∴y=﹣![]() ;
;
(2)
∵P(2,﹣4),Q(2,0)
∴PQ=4,过M作MN⊥PQ于N.
则 ![]() PQMN=6,
PQMN=6,
∴MN=3,
设M(x,﹣![]() ),
),
则 x=2+3=5或x=2﹣3=﹣1
当x=5时,﹣![]() =﹣
=﹣![]() ,
,
当x=﹣1时,﹣![]() =1,
=1,
∴M(5,﹣![]() )或(﹣1,8).
)或(﹣1,8).
故答案为:(1)y=﹣![]() ;(2)M(5,﹣
;(2)M(5,﹣![]() )或(﹣1,8).
)或(﹣1,8).

练习册系列答案
 新卷王期末冲刺100分系列答案
新卷王期末冲刺100分系列答案 全能闯关100分系列答案
全能闯关100分系列答案
相关题目