题目内容
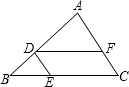
如图2,在□ABCD中,E是BC的中点,且
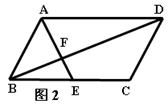
∠AEC=∠DCE,则下列结论不正确的是( )

∠AEC=∠DCE,则下列结论不正确的是( )
| A.S△AFD=2S△EFB | B.BF=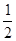 DF DF |
| C.四边形AECD是等腰梯形 | D.∠AEB=∠ADC |
A
分析:本题要综合分析,但主要依据都是平行四边形的性质.
解答:解:A、∵AD∥BC
∴△AFD∽△EFB
∴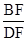 =
=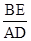 =
=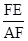 =
=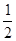
故S△AFD=4S△EFB;
B、由A中的相似比可知,BF=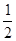 DF,正确.
DF,正确.
C、由∠AEC=∠DCE可知正确.
D、利用等腰三角形和平行的性质即可证明.
故选A.
解答:解:A、∵AD∥BC
∴△AFD∽△EFB
∴
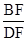 =
=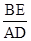 =
=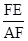 =
=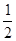
故S△AFD=4S△EFB;
B、由A中的相似比可知,BF=
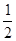 DF,正确.
DF,正确.C、由∠AEC=∠DCE可知正确.
D、利用等腰三角形和平行的性质即可证明.
故选A.

练习册系列答案
相关题目
 ,若AD︰BC = 2︰3. 请探究:当k为下列三种情况时,四边形ABPE是什么四边形?
,若AD︰BC = 2︰3. 请探究:当k为下列三种情况时,四边形ABPE是什么四边形?

 ,OA的长为半径的圆交边CD于点M,连接OM,过点M作圆O的切线交边BC于点N.
,OA的长为半径的圆交边CD于点M,连接OM,过点M作圆O的切线交边BC于点N.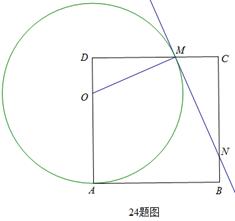
 , EF⊥DE
, EF⊥DE 的长;
的长; 的长.
的长.
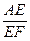 的值.
的值.
 ,且AB∶
,且AB∶ =1∶2 ,已知BC=8,则
=1∶2 ,已知BC=8,则 的长是( )
的长是( ) 中,
中,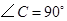 ,
,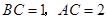 ,把边长分别为
,把边长分别为 的
的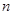 个正方形依次放入
个正方形依次放入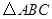 中,请回答下列问题:
中,请回答下列问题:
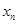
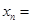 ;
;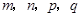 是正整数,且
是正整数,且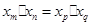 ,试判断
,试判断