题目内容
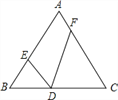
【题目】如图,在等边△ABC中,边长为6,D是BC边上的动点,∠EDF=60°.
(1)求证:△BDE∽△CFD;
(2)当BD=1,CF=3时,求BE的长.
【答案】(1)证明见解析;(2) ![]()
【解析】试题分析:
(1)由题意可得,∠B=∠C=60°,∠BDE+∠CDF=120°,∠BDE+∠BED=120°,由此可得:∠CDF=∠BED,从而可得:△BDE∽△CFD;
(2)由△BDE∽△CFD可得: ![]() ,由已知易得:CD=BC-BD=5-1=4,由此可得:
,由已知易得:CD=BC-BD=5-1=4,由此可得: ![]() ,解得BE=
,解得BE=![]() .
.
试题解析:
(1)∵△ABC是等边三角形,
∴∠B=∠C=60°,
∴∠BDE+∠BED=120°.
∵∠EDF=60°,
∴∠BDE+∠CDF=120°,
∴∠CDF=∠BED,
∴△BDE∽△CFD;
(2)∵等边△ABC的边长为5,BD=1,
∴CD=BC-BD=4.
∵△BDE∽△CFD,
∴![]() ,即
,即![]() ,
,
∴BE=![]() .
.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目