题目内容
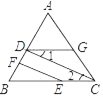
【题目】如图,已知DE∥BC,CD是∠ACB的平分线,∠ADE=70°,∠ACB=40°,求∠EDC和∠BDC的度数.

【答案】∠EDC=20°,∠BDC=90°.
【解析】
首先根据角平分线的性质可得∠DCB=20°,再根据DE∥BC,可得∠B=∠ADE=70°,然后根据平行线的性质可得∠EDC=∠BCD=20°,再根据三角形内角和定理可计算出∠BDC的度数.
解:∵CD是∠ACB的平分线,∠ACB=40°,
∴∠BCD=![]() ∠ACB=20°,
∠ACB=20°,
∵DE∥BC,∠ADE=70°,
∴∠B=70°,∠EDC=∠DCB=20°,∠BDE+∠B=180°,
∴∠BDE=110°,
∴∠BDC=∠BDE﹣∠EDC=110°﹣20°=90°.
∴∠EDC=20°,∠BDC=90°.

练习册系列答案
相关题目
【题目】如图,在矩形ABCD中,AB=6m,BC=12m,点P从点A出发沿AB边向B以1m/s的速度运动,同时点Q从点B出发,沿BC边向点C以2m/s的速度运动,P、Q两点在分别到达B、C两点后就停止运动,设经过ts时,△PBQ的面积为Sm2,则

(1)S与t的函数解析式为:S=_________;
(2)用表格表示:
t/s | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
S/m2 |
(3)用图象表示:
(4)在这个问题中,自变量t的取值范围是______;图象的对称轴是_______,顶点坐标是________;当t<______时,S的值随t值的增大而_______;当t>______时,S的值随t值的增大而_______(填“增大”或“减小”);当t=______时,S取得最大值为_______.