题目内容
 如图,在?ABCD中,E是BC的中点,且∠AEC=∠DCE,下列结论中正确的有( )
如图,在?ABCD中,E是BC的中点,且∠AEC=∠DCE,下列结论中正确的有( )①BF=
| 1 |
| 2 |
③四边形AECD是等腰梯形 ④∠AEB=∠ADC.
分析:根据已知条件即可推出△BEF∽△DAF,推出①为正确,②选项错误,利用已知条件可以推出四边形AECD为等腰梯形,推出③项正确,结合平行四边形的性质,可以推出④项正确.
解答:解:∵AD∥BC
∴△AFD∽△EFB
∴
=
=
=
;
故①BF=
DF,故此选项正确.
故S△AFD=4S△EFB,故 ②S△AFD=2S△EFB错误;
由∠AEC=∠DCE可知④∠AEB=∠ADC正确;
∵∠AEC=∠DCE,AD∥EC,
∴四边形AECD为等腰梯形,故③四边形AECD是等腰梯形正确.
故正确的有3个,
故选:C.
∴△AFD∽△EFB
∴
| BF |
| DF |
| BE |
| AD |
| EF |
| AF |
| 1 |
| 2 |
故①BF=
| 1 |
| 2 |
故S△AFD=4S△EFB,故 ②S△AFD=2S△EFB错误;
由∠AEC=∠DCE可知④∠AEB=∠ADC正确;
∵∠AEC=∠DCE,AD∥EC,
∴四边形AECD为等腰梯形,故③四边形AECD是等腰梯形正确.
故正确的有3个,
故选:C.
点评:此题主要考查了平行四边形的性质以及相似三角形的判定与性质等腰梯形的判定等知识,解决本题的关键是利用相似求得各对应线段的比例关系.

练习册系列答案
相关题目
 如图,在?ABCD中,对角线AC、BD相交于点O,AB=
如图,在?ABCD中,对角线AC、BD相交于点O,AB=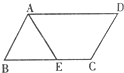 18、如图,在?ABCD中,∠A的平分线交BC于点E,若AB=10cm,AD=14cm,则EC=
18、如图,在?ABCD中,∠A的平分线交BC于点E,若AB=10cm,AD=14cm,则EC=
 (2011•犍为县模拟)甲题:已知关于x的一元二次方程x2=2(1-m)x-m2的两实数根为x1,x2.
(2011•犍为县模拟)甲题:已知关于x的一元二次方程x2=2(1-m)x-m2的两实数根为x1,x2.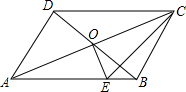 如图,在?ABCD中,∠ADB=90°,CA=10,DB=6,OE⊥AC于点O,连接CE,则△CBE的周长是
如图,在?ABCD中,∠ADB=90°,CA=10,DB=6,OE⊥AC于点O,连接CE,则△CBE的周长是