题目内容
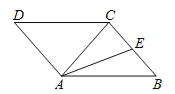
【题目】如图,在ABCD中,AC为对角线,AC=BC=5,AB=6,AE是△ABC的中线.
(1)用无刻度的直尺画出△ABC的高CH(保留画图痕迹);
(2)求△ACE的面积.
【答案】(1)作图见解析;(2)6.
【解析】(1)如图,连接BD,BD与AE交于点F,连接CF并延长到AB,则它与AB的交点即为H.
理由如下:
∵BD、AC是ABCD的对角线,∴点O是AC的中点,∵AE、BO是等腰△ABC两腰上的中线,∴AE=BO,AO=BE,∵AO=BE,∴△ABO≌△BAE(SSS),∴∠ABO=∠BAE,△ABF中,∵∠FAB=∠FBA,∴FA=FB,∵∠BAC=∠ABC,∴∠EAC=∠OBC,∵AC=BC,∠EAC=∠OBC,FA=FB,可得△AFC≌BFC(SAS),∴∠ACF=∠BCF,即CH是等腰△ABC顶角平分线,所以CH是△ABC的高;
(2)∵AC=BC=5,AB=6,CH⊥AB,∴AH=![]() AB=3,∴CH=
AB=3,∴CH=![]() =4,∴S△ABC=
=4,∴S△ABC=![]() ABCH=
ABCH=![]() ×6×4=12,∵AE是△ABC的中线,∴S△ACE=
×6×4=12,∵AE是△ABC的中线,∴S△ACE=![]() S△ABC=6.
S△ABC=6.


练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目