题目内容
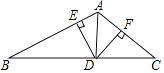
【题目】如图,在△ABC中,AB=AC , D为边BC上一点,以AB、BD为邻边作平行四边形ABDE , 连接AD、EC . 若BD=CD , 求证:四边形ADCE是矩形.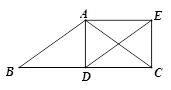
【答案】证明:∵AB=AC,BD=CD ,
∴AD⊥BC,
∴∠ADC=90°,
∵四边形ABDE是平行四边形,
∴AE∥BD,AE=BD,
∴AE∥CD,AE=CD,
∴四边形ADCE是平行四边形,
又∵∠ADC=90°,
∴四边形ADCE是矩形.
【解析】先证明四边形ADCE是平行四边形,再证一个角是直角,即可证得.
【考点精析】掌握矩形的判定方法是解答本题的根本,需要知道有一个角是直角的平行四边形叫做矩形;有三个角是直角的四边形是矩形;两条对角线相等的平行四边形是矩形.

练习册系列答案
相关题目